概述
LO DIV是位于VCO和mixer之间的模块,其作用是分频和驱动长走线,设计难点在于底噪。
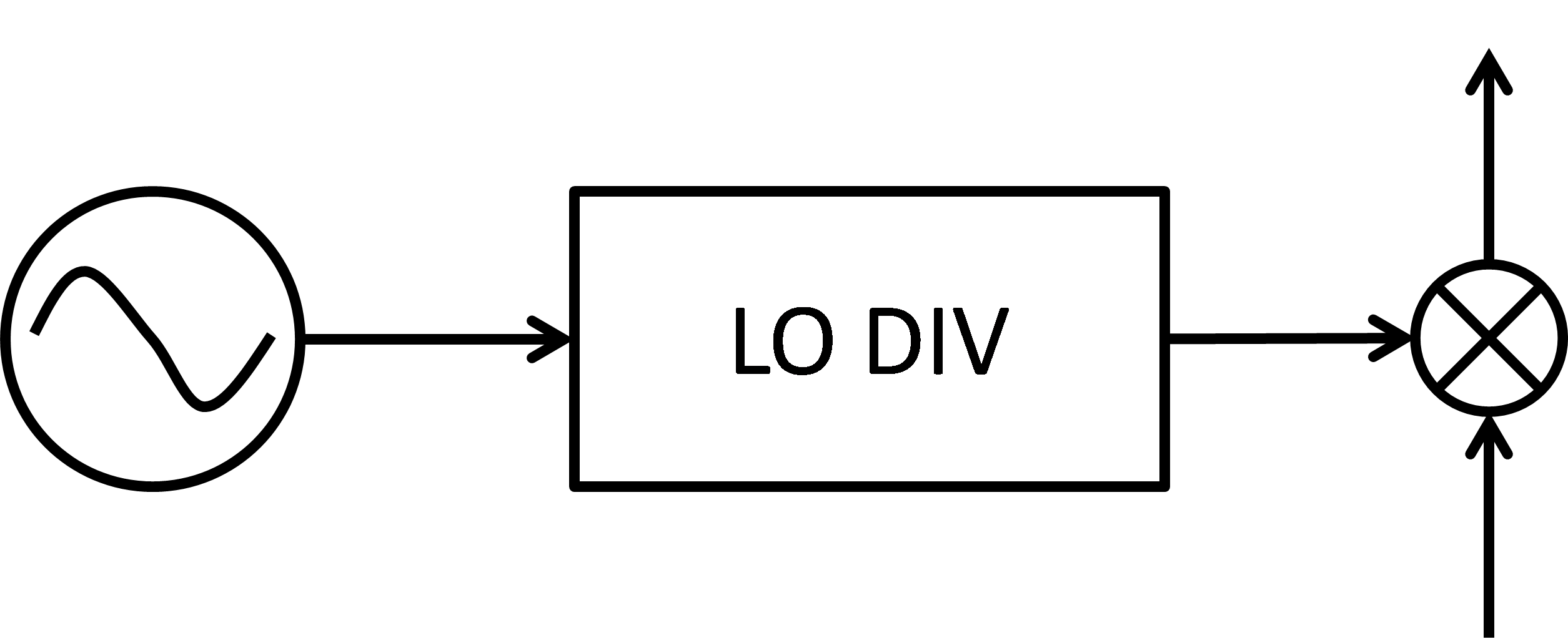
不同的band有不同的频率覆盖范围,为了减小VCO的设计难度需要选择合适的分频方案。E-UTRA规定的band与频率的对应关系在3GPP或wikipedia上可以查到。
一般来说,决定了所要支持的band、分频比步长、基本分频器、VCO的最高频率以及VCO的个数,最佳的LO分频方案就确定了。
- 所要支持的band决定于产品的定位,不需多说。
- 分频比步长决定于mixer结构,即如果需要正交时钟就至少有个除2,如果需要8相位时钟就至少有个除4,这项选择会非常大的影响能选用的方案。
- 基本分频器决定于技术储备,如果不能驾驭除3、除5那就老老实实的只用除2吧。
- VCO的最高频率决定于所用工艺,频率越高对寄生约敏感,暂以40nm工艺8GHz为上限进行讨论,实际能做多高还要看VCO设计工程师的水平。
- VCO的个数决定于规划的最大面积,也就是用成本换性能。
在选取方案时最重要的一个考虑项是VCO所需的调谐范围,这是因为宽调谐范围通常意味着小Q值的电感,即较差的相位噪声。如果两个VCO的话还可以考虑把对噪声要求高的band都放在一个调谐范围小的core里。
单core方案
由所需覆盖的分频后的频率范围和设定的VCO最高频率可以得出可用的最大分频比,再由分频比步长和可用的基本分频器种类得出真正可用的所有分频比。(此处把f_max调整到了8080MHz,是因为max(f_h)*4=8080,若不调整会出现无法全面遍历的问题)
% Up-link, f_max=8GHz, /2 could be used, /2 at least needed
f_l = [1920, 1850, 1710, 1710, 824, 2500, 880, 1749.9, 1710, 1427.9, 699, 777, 788, 704, 815, 830, 832, 1447.9, 3410, 2000, 1626.5, 1850, 814, 807, 703, 2305, 452.5];
f_h = [1980, 1910, 1785, 1755, 849, 2570, 915, 1784.9, 1770, 1447.9, 716, 787, 798, 716, 830, 845, 862, 1462.9, 3490, 2020, 1660.5, 1915, 849, 824, 748, 2315, 457.5];
f_max = 8080;
div_max= ceil(f_max/min(f_h));
basic_div = [2];
divs = [];
for i=2:2:div_max
tmp = unique(factor(i));
flag= 0;
for j=1:1:length(tmp)
if nnz(basic_div-tmp(j))==length(basic_div)
flag = 1;
break;
end
end
if flag==0
divs(end+1) = i;
end
end
得到了所有可用的分频比后就可以进行迭代了,初始方案为全都是最小分频比,后面的方案均继承前一个方案,然后调高限制最低频率的band的分频比,直到VCO的最高频率超过设置的f_max或限制最低频率的band的分频比已是最大值。
i = 1;
while 1
if i==1
plans(i, :) = divs(1)*ones(size(f_l));
else
plans(i, :) = plans(i-1, :);
for j=1:length(i_l)
plans(i, i_l(j)) = next_div(divs, plans(i, i_l(j)), +1);
end
end
[f_vco_l(i), f_vco_h(i), f_vco_range(i), i_l, i_h] = ...
check_plan(f_l, f_h, plans(i,:));
if f_vco_h(i)>f_max || max(plans(i, i_l))==divs(end)
break;
end
i = i+1;
end
最后按照VCO调谐范围进行排序,即可找到调谐范围最小时的分频方案。本例的结果如下图所示,VCO的调谐范围需要55%左右,难以实现。
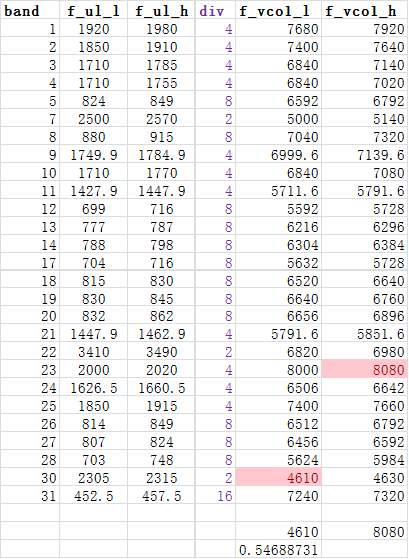
对于无法接受的结果可以通过增加VCO个数、提高VCO最高频率或采用/3/5分频器改善(若限制不在大分频比的band,采用/3/5分频器也没有作用,如本例),其中增加VCO个数是最直接、最有效的解决方法,缺点是会增加成本。
双core方案
增加一个VCO有时候不仅仅是增大了一个VCO的面积,还带来了布局布线上的困难,实在是不得已的办法。
对于两个VCO,首先要确定的是哪些band放到core1,哪些band放到core2。很直接的想到了遍历,但是分法的数量随着band个数的增加呈指数形式($n=\sum_{i=0}^{floor(k/2)} C_{k}^{i}$),以本例中的27个band来说就有67M种分法,遍历的困难太大。
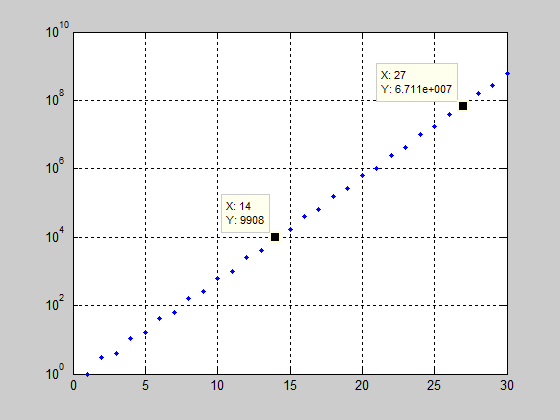
把f_l和f_h按照大小顺序画出来会发现有很多band的频率范围是相近的,可以把它们分成一组,通过这种方法来大大减少分法。
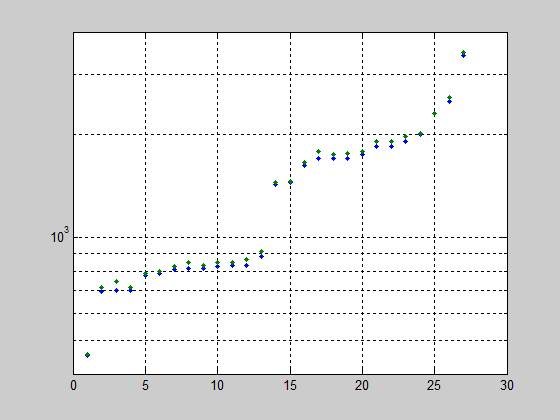
因此双core方案的遍历方法是:
- 通过
分组->组合->映射回band的方法把所有的分法都列出来; - 依次求出每种分法的core1和core2的最佳方案;
- 以两个core的频率范围中的较大值作为当前分法的频率范围,进行排序,找出最佳方案。
具体实现代码如下:
f_l = [1920, 1850, 1710, 1710, 824, 2500, 880, 1749.9, 1710, 1427.9, 699, 777, 788, 704, 815, 830, 832, 1447.9, 3410, 2000, 1626.5, 1850, 814, 807, 703, 2305, 452.5];
f_h = [1980, 1910, 1785, 1755, 849, 2570, 915, 1784.9, 1770, 1447.9, 716, 787, 798, 716, 830, 845, 862, 1462.9, 3490, 2020, 1660.5, 1915, 849, 824, 748, 2315, 457.5];
group = [10, 9, 8, 8, 4, 13, 5, 8, 8, 6, 2, 3, 3, 2, 4, 4, 4, 6, 14, 11, 7, 9, 4, 4, 2, 12, 1];
% 根据分组进行组合
u_group = unique(sort(group));
l_choose_group = 0;
for i=0:floor(length(u_group)/2)
l_choose_group = l_choose_group+nchoosek(length(u_group), i);
end
choose_group= zeros(l_choose_group, length(u_group));
k = 1;
for i=0:floor(length(u_group)/2)
tmp = nchoosek(u_group, i);
if isempty(tmp)
choose_group(k, :) = ones(size(u_group));
k = k+1;
else
for j=1:length(tmp(:,1))
choose_group(k, :) = ones(size(u_group));
choose_group(k, tmp(j,:)) = 2;
k = k+1;
end
end
end
% 把组合结果映射回band
sel_core = ones(length(choose_group(:,1)), length(group));
for i=1:length(choose_group(:,1))
tmp = find(choose_group(i,:)==2);
if ~isempty(tmp)
for j=1:length(tmp)
sel_core(i, group==tmp(j)) = 2;
end
end
end
fprintf('\t分组完成,共计%d条。\n', length(sel_core(:,1)));
fprintf('\t开始遍历:');
% 逐条进行freq plan遍历,并将最好的方案汇总在一起
plans = zeros(size(sel_core));
f_vco1_range= zeros(length(sel_core(:,1)), 1);
f_vco1_l = zeros(length(sel_core(:,1)), 1);
f_vco1_h = zeros(length(sel_core(:,1)), 1);
f_vco2_range= zeros(length(sel_core(:,1)), 1);
f_vco2_l = zeros(length(sel_core(:,1)), 1);
f_vco2_h = zeros(length(sel_core(:,1)), 1);
f_vco_range = zeros(length(sel_core(:,1)), 1);
for i=1:length(sel_core(:,1))
if mod(i, round(length(sel_core(:,1))/10))==0
fprintf('.....%d%%', round(i*100/round(length(sel_core(:,1)))));
end
i1 = find(sel_core(i,:)==1);
i2 = find(sel_core(i,:)==2);
if ~isempty(i1)
[tplans, tf_vco_range, tf_vco_l, tf_vco_h] = ...
do_freq_plan(f_l(i1), f_h(i1));
[tmp, j] = sort(tf_vco_range, 2, 'ascend');
plans(i, i1) = tplans(j(1),:);
f_vco1_range(i) = tf_vco_range(j(1));
f_vco1_l(i) = tf_vco_l(j(1));
f_vco1_h(i) = tf_vco_h(j(1));
end
if ~isempty(i2)
[tplans, tf_vco_range, tf_vco_l, tf_vco_h] = ...
do_freq_plan(f_l(i2), f_h(i2));
[tmp, j] = sort(tf_vco_range, 2, 'ascend');
plans(i, i2) = tplans(j(1),:);
f_vco2_range(i) = tf_vco_range(j(1));
f_vco2_l(i) = tf_vco_l(j(1));
f_vco2_h(i) = tf_vco_h(j(1));
end
f_vco_range(i) = max([f_vco1_range(i); f_vco2_range(i)]);
end
fprintf('.....100%%\n');
% 按照range升序排序
fprintf('\t== 单Core方案 ================================================\n');
fprintf('\tRange = %.3f, Fmin = %.1fMHz, Fmax = %.1fMHz, %s\n', ...
f_vco1_range(1)*100, f_vco1_l(1), f_vco1_h(1), num2str(plans(1, :)));
fprintf('\t== 双Core方案 ================================================\n');
j = find(f_vco_range==min(f_vco_range));
sel_core = sel_core(j, :);
plans = plans(j, :);
f_vco1_range = f_vco1_range(j);
f_vco1_l = f_vco1_l(j);
f_vco1_h = f_vco1_h(j);
f_vco2_range = f_vco2_range(j);
f_vco2_l = f_vco2_l(j);
f_vco2_h = f_vco2_h(j);
f_vco_range = min([f_vco1_range, f_vco2_range], [], 2);
[tmp, i] = sort(f_vco_range, 1, 'ascend');
for j=1:length(i)
fprintf('\tRange_1 = %.3f%%, Fmin_1 = %.1fMHz, Fmax_1 = %.1fMHz; Range_2 = %.3f%%, Fmin_2 = %.1fMHz, Fmax_2 = %.1fMHz; %s; %s\n', ...
f_vco1_range(i(j))*100, f_vco1_l(i(j)), f_vco1_h(i(j)), ...
f_vco2_range(i(j))*100, f_vco2_l(i(j)), f_vco2_h(i(j)), ...
num2str(sel_core(i(j), :)), num2str(plans(i(j), :)));
end
fprintf('\n');
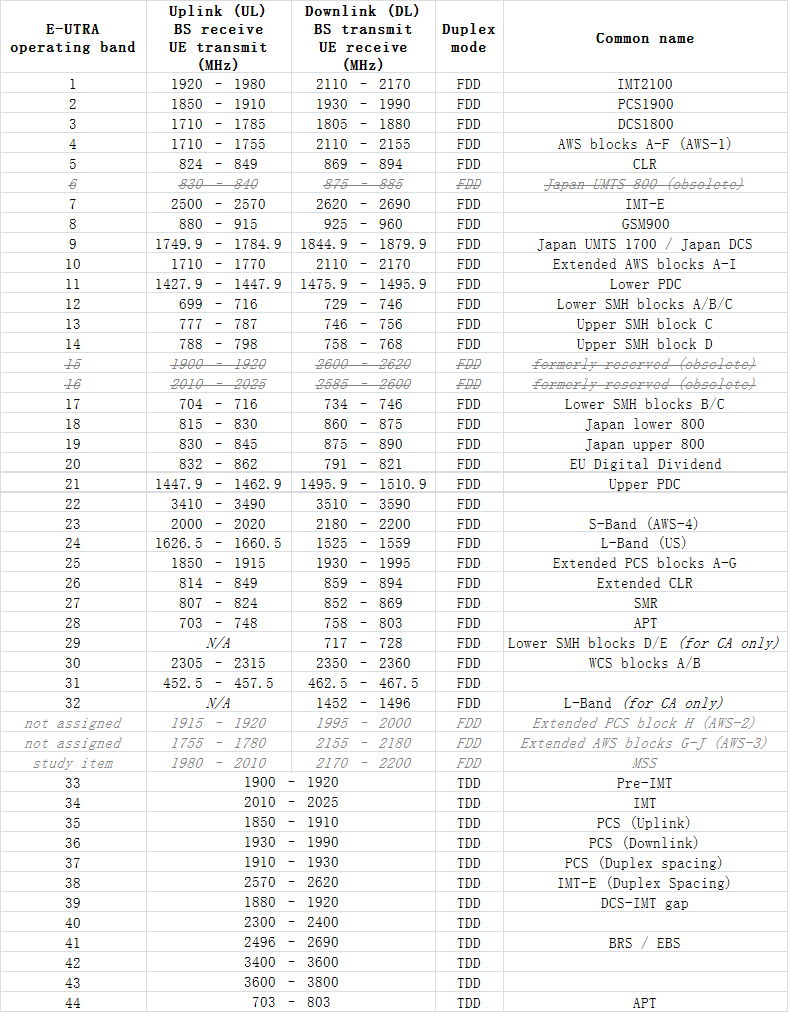
运行结果如下图所示:
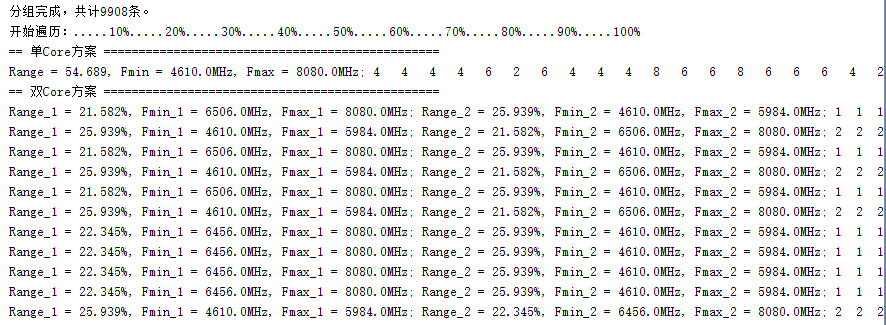
最终结果
Up-link的LO方案:
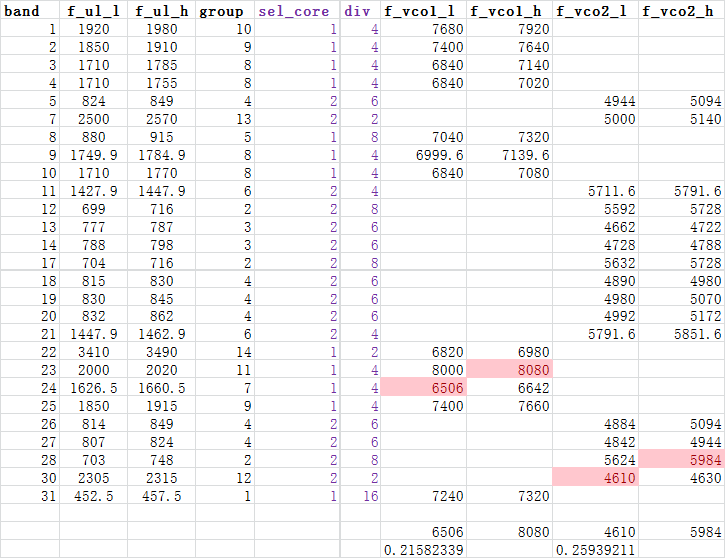
Down-link的LO方案(TDD模式的都放到了Down-link中):