SDM是PLL里很重要的一个噪声源,下面分析一下SDM对NDIV输出时钟相噪的影响。
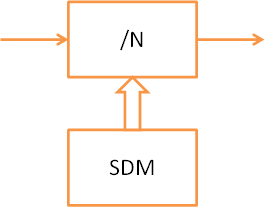
NDIV的输出
首先,SDM输出信号的噪声是量化噪声的$\mathrm{sdm\_order}$次差分(具体推导暂且不提),而量化噪声是在$[-f_s/2 , +f_s/2]$范围内均匀分布,噪声功率为$\Delta^2/12$,差分的传函是$1-z^{-1}$,则有
\[\begin{eqnarray} PSD_{SDM} &=& Qn \cdot [(1-z^{-1})^\mathrm{sdm\_order}]^2 \\ &=& \frac{1}{12\cdot f_s} \cdot [(1-z^{-1})^\mathrm{sdm\_order}]^2 \end{eqnarray}\]其中,$f_s = f_{ref}$。
然后,对于分频比序列$n[i]$,NDIV输出信号的上升沿位于
\[\begin{eqnarray} t[i] &=& t_0+\sum_i (n[i] \cdot Tvco) \\ &=& t_0+\sum_i((n_{avg}+n_{err}[i]) \cdot Tvco) \\ &=& t_0+i \cdot Tref+Tvco \cdot \sum_i n_{err}[i] \\ \end{eqnarray}\]显然有$t_{err}[i]=Tvco \cdot \sum_i n_{err}[i]$,由此可得NDIV输出信号的相位误差为
\[\begin{eqnarray} ph_{err}[i] &=& 2\pi \cdot \frac{t_{err}[i]}{Tref} \\ &=& 2\pi \cdot \frac{Tvco}{Tref} \cdot \sum_i n_{err}[i] \\ &=& \frac{2\pi}{n_{avg}} \cdot \sum_i n_{err}[i] \end{eqnarray}\]由上式可以看到SDM的噪声到NDIV的输出端有个累加过程,累加的传函是$1/(1-z^{-1})$,即抵消掉SDM的一个差分。
综上,NDIV输出的相位噪声(方便起见均未取$10 \log_{10}$,下同)为
\[PN_{NDIV} = {\frac{1}{12 \cdot f_{ref}} \cdot |(1-z^{-1})^{(\mathrm{sdm\_order}-1)}|^2 \cdot (\frac{2\pi}{n_{avg}})^2}\]最后放上理论值与仿真结果的对照:
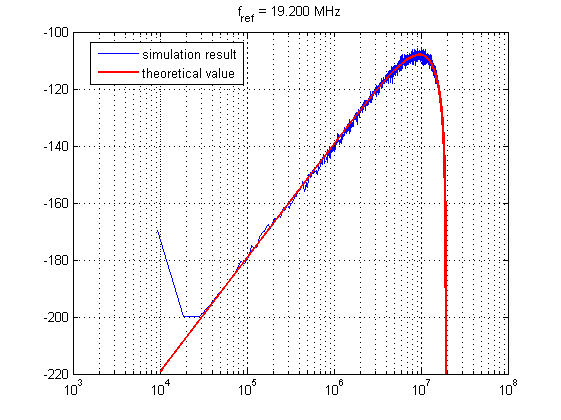
*注:此处的仿真结果为two-sided PSD。
VCO的输出
而到VCO输出端的噪声贡献为
\[PN_{OUT}|_{NDIV}=PN_{NDIV} \cdot |\frac{N \cdot Hol}{1+Hol}|^2\]其中$Hol$为PLL的不包括NDIV的开环传递函数,此处的$N$即为$n_{avg}$,带入$PN_{NDIV}$可得:
\[PN_{OUT}|_{NDIV} = \frac{1}{12 \cdot f_{ref}} \cdot |(1-z^{-1})^{(\mathrm{sdm\_order}-1)}|^2 \cdot |\frac{2\pi Hol}{1+Hol}|^2\]又由于在我们关心的频率处有$\vert 1-z^{-1}\vert \approx 2\pi f_{oft}/f_{ref}$,推导过程如下:
由$z = e^{s/f_{ref}}$和 $s = j\cdot2\pi f $,根据欧拉公式可得:
\[\begin{eqnarray} |1-z^{-1}| &=& |1-e^{-j \cdot 2\pi f/f_{ref}}| \\ &=& |1-\cos(2\pi f/f_{ref})+j \cdot \sin(2\pi f/f_{ref})| \\ &=& \sqrt{[1-\cos(2\pi f/f_{ref})]^2 + \sin^2(2\pi f/f_{ref})} \\ &=& \sqrt{2 \cdot [1-\cos(2\pi f/f_{ref})]} \\ &=& \sqrt{2 \cdot 2 \cdot \sin^2(\pi f/f_{ref})} \\ &=& 2 \cdot |\sin(\pi f/f_{ref})| \end{eqnarray}\]当$f=f_{oft} \ll f_{ref}/\pi$时,做等价无穷小代换可得:
\[|1-z^{-1}| \approx 2\pi f_{oft}/f_{ref}\]
则有
\[PN_{OUT}|_{NDIV} \approx \frac{1}{12} \cdot \left(\frac{2\pi f_{oft}}{f_{ref}} \right)^{2\cdot \mathrm{sdm\_order}-1} \cdot |\frac{2\pi Hol}{1+Hol}|^2\]因此,若保持$fvco$不变的情况下增大一倍$fref$,对于3阶SDM引入的噪声:
- 在低频偏处噪声降低15dB;
- 噪声峰值降低3dB;
- 峰值所在的频率增大一倍(更容易被环路滤波器抑制)。
Update @2021-05-26: 补充$ph_{err}[i]$的推导过程和对VCO输出端的噪声贡献。
Update @2022-05-08: 修正结论,并使用eqnarray整理方程式组。
