自从加入M记后,开始比较密集的接触关于jitter的相关内容,并且发现有很多同事并不能很清楚的认识到jitter的分类和应用。通过查询各方面的资料,整理本文如下,以备不时之需。
概述
Jitter(抖动)是从时域评价时钟信号质量的重要参数。
- 首先要明确的是它是一个统计量,因此有标准差(均方根,rms)和范围(峰峰值,p2p);
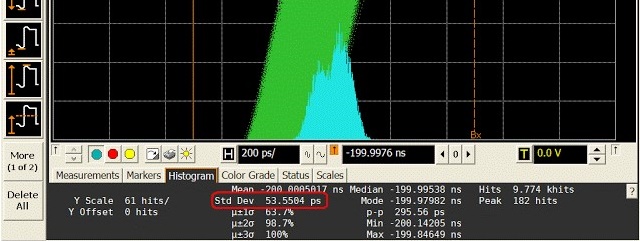
- 然后根据样本的类型可以划分成不同的分类,如Jabs(absolute jitter)、Jp(period jitter)、Jc2c(cycle-to-cycle jitter)等;
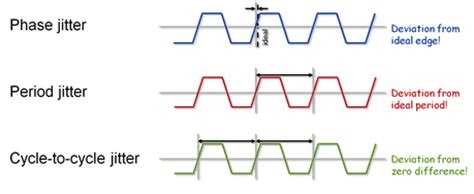
- 再次是对于同一次统计又可以从中拆分出不同的构成(成分),如bounded jitter和unbounded jitter。其中一般认为unbounded jitter是呈高斯分布的,因此在计算峰峰值时会根据误码率(BER)将均方根值乘以一个系数。
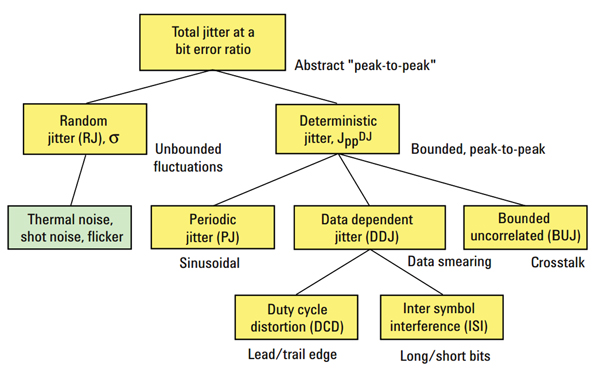
另外,要明确的是在jitter的分类中,存在着一定的歧义或别名,如absolute jitter也被称为phase jitter,period jitter也被称为cycle jitter等等。
与相位噪声的关系
Phase noise(相位噪声)是从频域评价时钟信号质量的重要参数。因此对于同一个时钟信号既可以用相噪来进行描述,也可以用jitter来进行描述。一般来说phase noise曲线包含的信息量更大,也更方便与设计进行比对,但出于方便应用的目的,通常需要根据应用转换为相应类型的jitter。
理论上讲,jitter只关注了时钟跳变沿的噪声情况,phase noise则应当关注全频带的噪声,但目前的应用中基本上都是用类方波信号作为时钟源,所以二者所关注的噪声范围并没有太多的差异。
Phase noise到jitter的转换是通过积分相噪(IPN)进行的,具体的可以参考之前的文章由相位噪声曲线计算积分相噪和Jitter的方法。
绝对抖动(absolute jitter, Jabs)
Jabs所统计的对象是实际时钟跳变沿出现的时刻与理想时钟跳变沿出现的时刻之间的差,因此也叫phase jitter,如下图所示。(注:实际测试中没有所谓的理想时钟,一般指的是被测信号的线性回归值,下同)
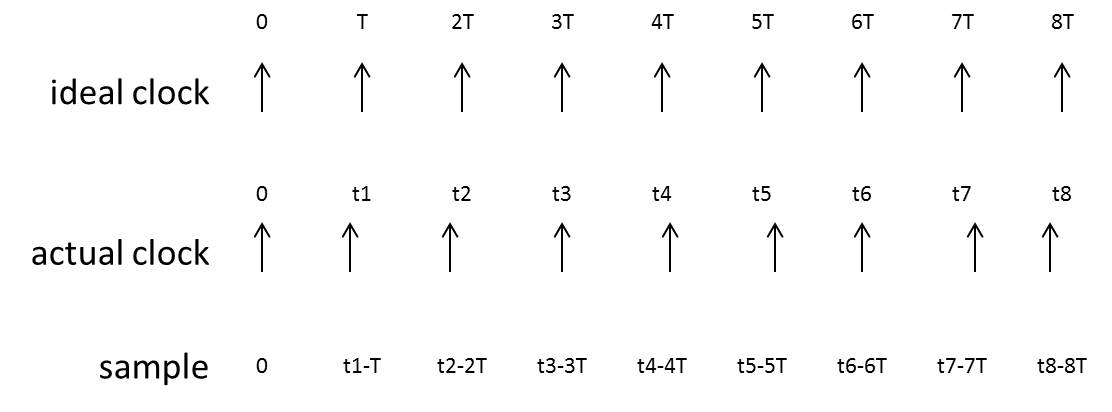
一般ADC、DAC应用关心这类jitter的rms值。
通过Phase noise曲线计算Jabs时,只需要把曲线下方的面积计算出来换算即可。
\[Jabs_{rms}^2=\frac{1}{(2\pi f_c)^2}\int_0^\infty{2L(f)df}\]其中\(L(f)\)为单边带相位噪声(SSB Phase Noise)。
另外,从定义也很容易得出,对于主要能量集中于低频偏部分的场景(一般情况下都能满足),经过分频的时钟的Jabs是不变的。
周期抖动(period jitter, Jp)
Jp所统计的对象是相邻两个实际时钟跳变沿出现的时间间隔与理论值的差或实际时钟周期与理想时钟周期的差,在测试中所谓理想时钟周期即是平均时钟周期,如下图所示:
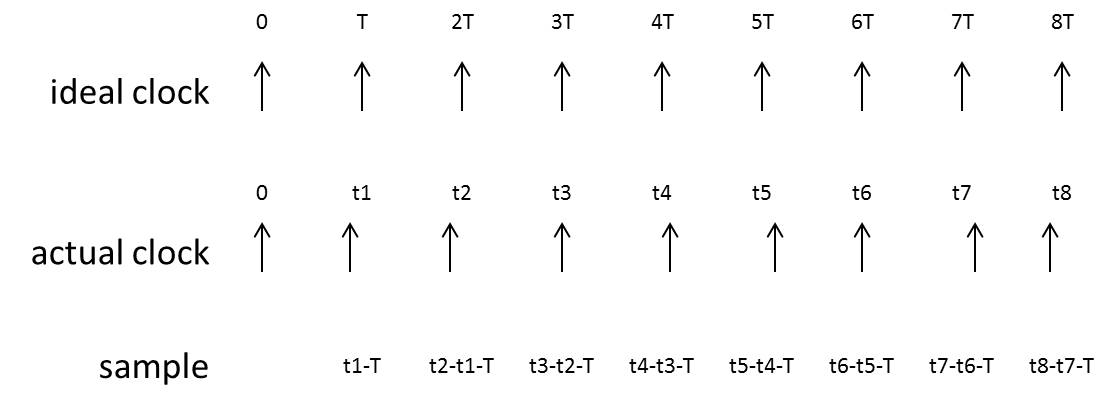
一般在数字电路(如MCU、CPU)应用中关心这类jitter的峰峰值。
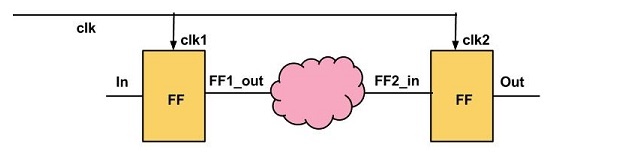
以上图所示的电路为例(为方便计算,假设clk1、clk2均为理想的clk),则有
\[t_{setup}=t_{n+1}-(t_n+t_{ck-q}+t_{comb})=T_{clk}-t_{jitter\_p2p}-t_{ck-q}-t_{comb}\]因此Jp的峰峰值会造成\(t_{setup}\)的减小。
对于随机抖动(random jitter),一般认为其呈高斯分布,那么峰峰值与RMS值的关系为
\[Jitter_{p2p}=\alpha Jitter_{rms}\]其中\(\alpha\)由\(\frac{1}{2}erfc(\frac{\alpha}{2\sqrt(2)})=BER\)确定,常见的取值见下表:
| BER | \(\alpha\) |
|---|---|
| \(10^{-3}\) | 6.180 |
| \(10^{-4}\) | 7.438 |
| \(10^{-5}\) | 8.530 |
| \(10^{-6}\) | 9.507 |
| \(10^{-7}\) | 10.399 |
| \(10^{-8}\) | 11.224 |
| \(10^{-9}\) | 11.996 |
| \(10^{-10}\) | 12.723 |
| \(10^{-11}\) | 13.412 |
| \(10^{-12}\) | 14.069 |
| \(10^{-13}\) | 14.698 |
| \(10^{-14}\) | 15.301 |
| \(10^{-15}\) | 15.883 |
| \(10^{-16}\) | 16.444 |
通过Phase noise曲线计算Jabs时,需要考虑\(t_n-t_{n-1}\)带来的影响,因此需要在原始的曲线上叠加一个权重曲线。
\[Jp_{rms}^2=\frac{1}{(\pi f_c)^2}\int_0^\infty{2L(f) \sin^2(\pi f/f_c)df}\]在计算时可以发现,这条权重曲线几乎抑制了所有的低频噪声,使得Jp由底噪所主导。
相邻周期抖动(cycle-to-cycle jitter, Jc2c)
Jc2c所统计的对象是相邻两个实际时钟周期之间的差,如下图所示:
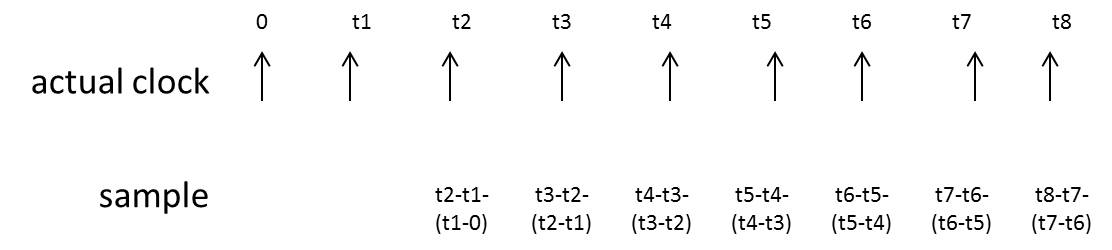
显然这类jitter不需要参考理想时钟,一般在并行接口应用中关心它的峰峰值。
通过Phase noise曲线计算Jc2c时,需要考虑两次差分带来的影响,即:
\[Jc2c_{rms}^2=\frac{4}{(\pi f_c)^2}\int_0^\infty{2L(f) \sin^4(\pi f/f_c)df}\]与Jp相类似的,两次差分引入的权重曲线进一步抑制了低频噪声,使得Jc2c也是由底噪所主导。
累计抖动(accumulating jitter, Jacc)
Jacc所统计的对象是相距k个时钟跳变沿的时间间隔与理论值的差,显然当k=1时即是Jp,当k=∞时即是Jabs。
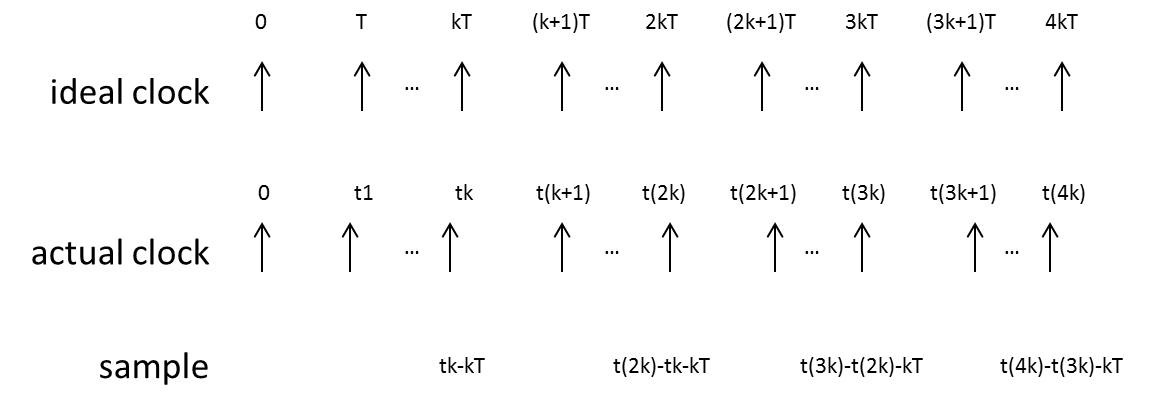
对于提供同步时钟,但时钟频率低于数据速率的场景会关心累计抖动。
通过Phase noise曲线计算k个周期的Jacc的公式如下:
\[Jacc_{rms}(k)^2=\frac{1}{(\pi f_c)^2}\int_0^\infty{2L(f) \sin^2(k\pi f/f_c)df}\]CDR后的抖动
对于给SerDes Tx提供驱动的时钟来说,其jitter大小要把CDR的影响考虑进来。
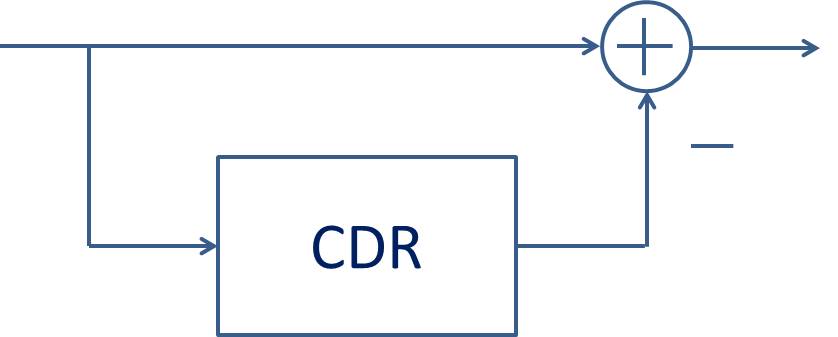
具体的在此不做详述,后续再写一篇梳理一下常见标准的CDR参数。
