Math

为什么增益裕度可以是负数

Posted by MaZhaoxin on June 8, 2019

引子

可能很多人都有过一个疑问，对于type-II PLL的传递函数（其波特图如下所示）而言，在DC处相移是180度，且开环增益远大于0dB，为什么还可以保持稳定呢？

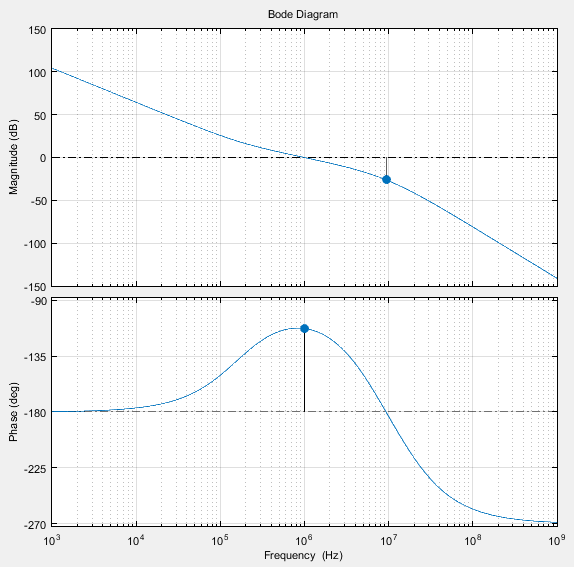
Bode_PLL_OL

如果说上例中DC处的180度相移是无限接近的话，在有温度补偿环路的PLL中（其频响曲线如下图所示），相频曲线明明白白地在增益大于0dB的位置穿过了180度，为什么还是能稳定呢？

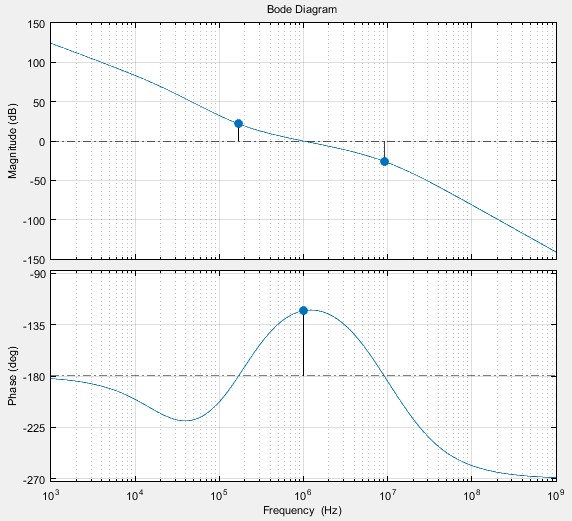
Bode_PLL_OL_wTempCal

或者换句话说，如果一个系统的相位裕度为正，但增益裕度为负，那么这个系统是稳定的吗？如果可以，增益裕度的意义是什么？

稳定性判据

基本概念

我们知道，线性时不变（LTI）系统均有对应的单位冲激响应$h(t)$，其拉普拉斯变换$H(s)$被称为系统函数或系统的传递函数。$H(s)$可以写成分子多项式比上分母多项式的形式（且分母的多项式阶数不小于分子多项式的阶数），分子多项式的根被称为零点，分母多项式的根被称为极点。

判断系统是否稳定的依据是观察系统的极点是否全部在复平面的左半平面。至于原因可参考：根轨迹极点在右边为什么不稳定？ -知乎，简单整理如下：

对LTI系统来说，系统稳定的定义为有限的输入对应有限的输出。而输出是输入和单位冲激响应的卷积：$y(x)=x(t)*h(t)$，那么就要求单位冲激响应$h(t)$是绝对可积的，也就是要求$h(t)$的傅立叶变换——系统的频率响应$H(j\omega)$是存在的。

根据拉普拉斯变换的相关性质，可以得到结论：系统稳定的充要条件是系统的极点的实部小于零（即位于左半平面）。

推导过程简化如下：

\[x(t)*h(t)有限 \rightarrow h(t)绝对可积 \rightarrow H(j\omega)=F\{h(t)\}存在 \rightarrow H(s)=L\{h(t)\}存在 \rightarrow 虚轴j\omega在L\{h(t)\}收敛域内\] \[因果系统 \rightarrow h(t)是右边信号 \rightarrow 若\sigma在收敛域内，则满足Re\{s\}\geq Re\{\sigma\}的s都在收敛域内 \rightarrow 收敛域在最右极点的右边（收敛域中没有极点）\]

结合上两个结论，既要虚轴在收敛域内，又要收敛域在最右极点的右边，只能要求极点的实部小于零。

考虑最简单的情况，有负反馈系统如下图所示（其中$H(s)=num(s)/den(s)$）：

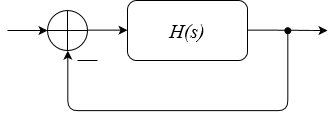
Diagram_Sample_Negative_Feedback

易得其闭环传递函数为$G(s)=H(s)/(1+H(s))=num(s)/(num(s)+den(s))$，显然有

  • 闭环传函的零点与开环传函的相同；
  • 闭环传函的极点由$num(s)+den(s)$即$1+H(s)$决定。

现在的问题就转化为，如何根据$H(s)$判断$1+H(s)$是否有在右半平面的根。

如果能写出$H(s)$的解析式，求解$1+H(s)=0$并不是什么难事。如果不能写出其解析式，该如何判断呢？

巴克豪森判据

巴克豪森判据（Barkhausen Stability Criterion）提供了一种简单的办法来判断系统的稳定性，它的出发点是假设有一个正弦激励信号在环路里走了一圈，如果回来的信号是同相的，且幅度没有变小，无论这个激励信号的频率如何，这个系统都是不稳定的。这种想法很直观，并且很容易利用波特图（Bode Plot）进行判断，是在线电等课程中最常见到的稳定性判据。

即对于前面提到的负反馈而言，$\angle H(s)=180^\circ$表示激励信号转一圈后是同相的，$\vert H(s)\vert \geq 1$表示回来的信号幅度相同或变大。

波特图描述的是当$s=j\omega$时，$\vert H(s)\vert $和$\angle H(s)$随$\omega$的变化情况，其中$\vert H(s)\vert $以dB为单位。对于特定的$\omega$，对应的$\vert H(j\omega)\vert $和$\angle H(j\omega)$即表示角频率为$\omega$的激励信号经过该系统传递后获得的增益和相移。因此可以在幅频曲线（$\vert H(j\omega)\vert -\omega$）和相频曲线（$\angle H(j\omega)-\omega$）上标出0dB和180$^\circ$的位置，借此判断由其构成的闭环系统是否稳定，以及裕量如何。

如下图所示，这个闭环系统是稳定的，并且其相位裕度（Phase Margin）是47$^\circ$，增益裕度（Gain Margin）是11.6dB。

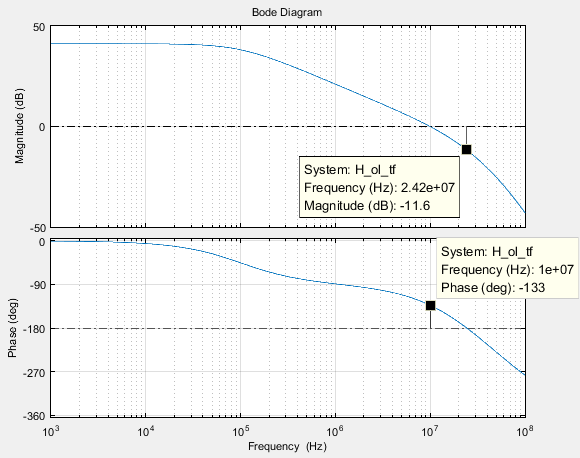
Bode_OPAMP

由于过冲（Overshooting）的大小与相位裕度有关（参考：Overshoot as a Function of Phase Margin），因此在实际应用中我们更多的用波特图观察相位裕度及其走向，而不太关注增益裕度。

如果出现了负的增益裕度，系统一定会像前面所述的那样出现不稳定的现象吗？给上面那个波特图在200kHz处加3个极点、在1MHz处加3个零点，会得到下面的图像（调整了增益项使单位增益频率不变）：

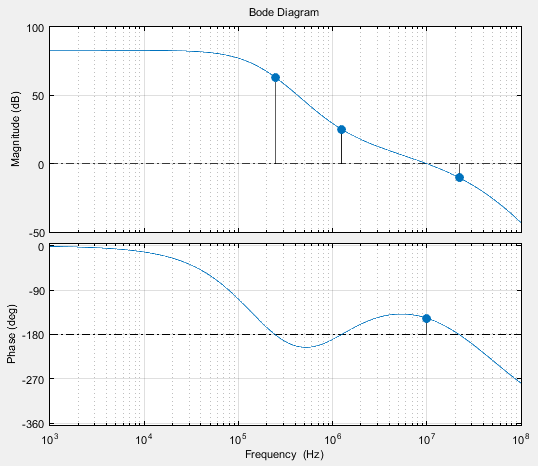
Bode_OPAMP_2

在上图中有3个增益裕度，其中两负一正（-63.3dB、-25.2dB和+10.2dB）。而基于这个开环传函构建的闭环系统是稳定的，因为它的极点均在左半平面：

>> pole(feedback(H_ol_tf, 1))

ans =

   1.0e+08 *

  -6.0843 + 0.0000i
  -3.8408 + 0.0000i
  -0.2917 + 0.7180i
  -0.2917 - 0.7180i
  -0.1148 + 0.0000i
  -0.0510 + 0.0103i
  -0.0510 - 0.0103i

检视闭环系统的阶跃响应也可以证明这点：

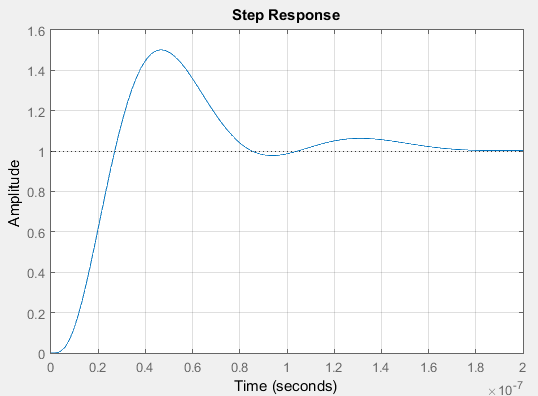
Step_OPAMP_2

这个例子说明巴克豪森判据对于这种问题是不完备的，它只能用于相频曲线只穿过一次180$^\circ$线的情况。更多的可以参考Barkhausen Stability Criterion。

根轨迹法

根轨迹（Root Locus）法是根据开环传函的零极点分布，通过改变其某个参数（一般是增益）来观察闭环极点在复平面上位置的变化情况，进而判断闭环系统稳定条件的方法。

根轨迹的绘制非常复杂和繁琐，具体的可以参考要想正确画出根轨迹，先搞清楚这8大法则再说！。不过借助MATLAB可以很轻松的获得上面那个传函的根轨迹图，如下所示（右侧的为局部放大图）：

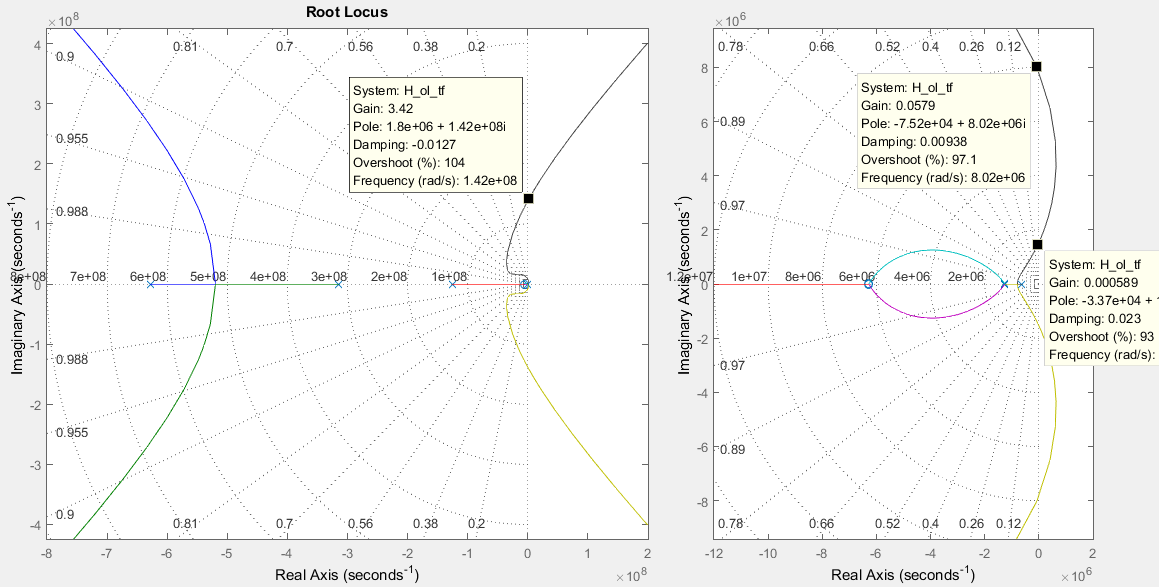
RLocus_OPAMP_2

从根轨迹图上可以看到闭环传函的极点有两部分到了右半平面，分别是

  • 当增益约大于3.42时（精确值是3.2359）；
  • 当增益约在0.000589～0.0579之间时（精确值是0.000684～0.0550）。

这正对应了前面的增益裕度（+10.2dB、-63.3dB和-25.2dB）。

也就是说，增益裕度的含义是如果环路的额外增益出现这样的变化的话，系统会进入不稳定状态。正的裕度表示环路的增益变大会导致不稳定，负的则表示增益变小会导致不稳定。而至于为何环路增益在环路相移为180$^\circ$时大于1却不会产生自激振荡，我还没有找到合理、直观的答案，可参考：

根轨迹法在实际应用中的问题在于需要知道传递函数的解析式，而如果知道了解析式便可以直接求解$1+H(s)=0$，因此我们还是希望直接利用$H(s)$的响应曲线进行判断，因为它是可以通过实验法获得的。

奈奎斯特判据

奈奎斯特判据（Nyquist Stability Criterion）利用了柯西副角定理（Cauchy’s argument principle），其简单的表述如下：

  • 若在$s$平面用闭合曲线顺时针包围$H(s)$的零点，则在$H(s)$平面原点会被顺时针包围；
  • 若在$s$平面用闭合曲线顺时针包围$H(s)$的极点，则在$H(s)$平面原点会被逆时针包围；
  • 若在$s$平面用闭合曲线不包围$H(s)$的零点或极点，则在$H(s)$平面原点不会被闭合曲线包围；
  • 若在$s$平面用闭合曲线顺时针包围$H(s)$的多个零点和极点，则在$H(s)$平面原点会被顺时针包围$N=Z-P$圈，其中$Z$为闭合曲线中零点的个数，$P$为闭合曲线中极点的个数，若$N$为负值则表示原点被逆时针包围；

基于副角定理可以推断，如果在$s$平面沿着虚轴从$-\infty$到$+\infty$、再沿着一个半径为无穷大的半圆回到$-\infty$，将覆盖$H(s)$所有在右半平面的零极点，那么数一数$H(s)$平面中原点被绕了几圈就可以推断右半平面零极点的个数。同样的道理，数一数点(-1, 0)被绕了几圈就可以推断$1+H(s)$右半平面零极点的个数，如下图所示（参考自奈奎斯特稳定判据）：

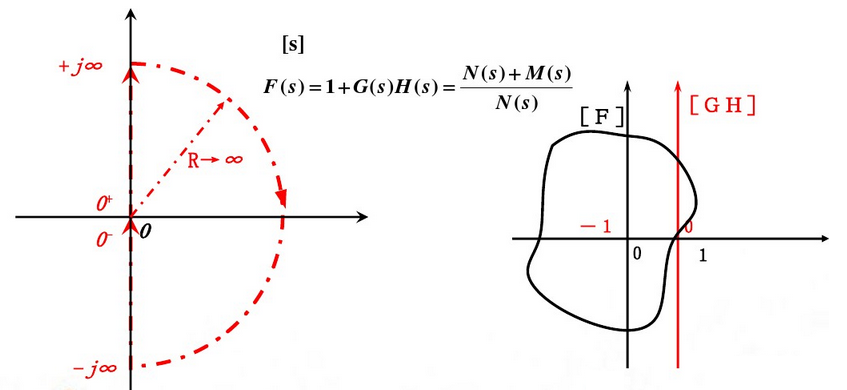
Nyquist_principle

注意这里有个前提条件是原点和虚轴上没有零极点。

如果开环传函没有右半平面零极点（即$P=0, Z=0$），那么闭环系统稳定的充要条件是曲线不包围点(-1, 0)。

对于开环传函有原点处极点的情况（例如PLL的传函），则需要补全曲线，其规则是用一个半径为无穷大的圆弧从正半实轴连接到$\omega=0^+$的点，圆弧的角度为$-n\cdot\pi/2$，其中$n$为开环传函中位于原点的极点个数。下图所示的为$n$分别取1、2、3的情况（从波特图上理解，可以认为在最最左侧相位从0连续变到$-n\cdot\pi/2$，即在相频曲线上画了一条竖线）：

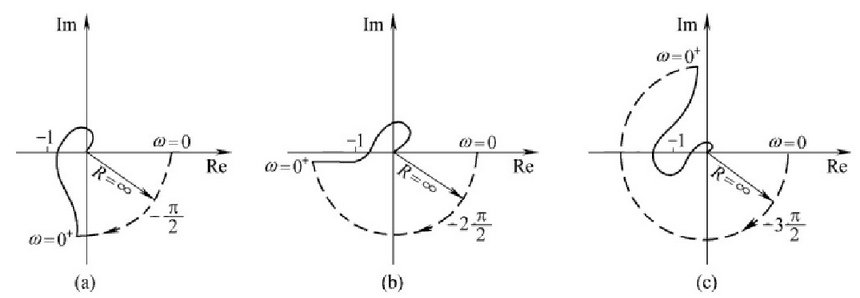
Nyquist_principle_2

因为$H(a-jb)$与$H(a+jb)$的实部相同、虚部互为相反数（即关于实轴对称），实际应用中只需要知道$\omega=0^+\rightarrow+\infty$的情况即可。具体的可以参考：

例1：把前面那个系统的$H(s)$在$s=j\omega, \omega=0\rightarrow+\infty$的值在复平面上画出，并对其做关于实轴的镜像，即得到了奈奎斯特图。在查看奈奎斯特图时需要不同级别的缩放，以观察曲线和点(-1, 0)的关系，如下图所示：

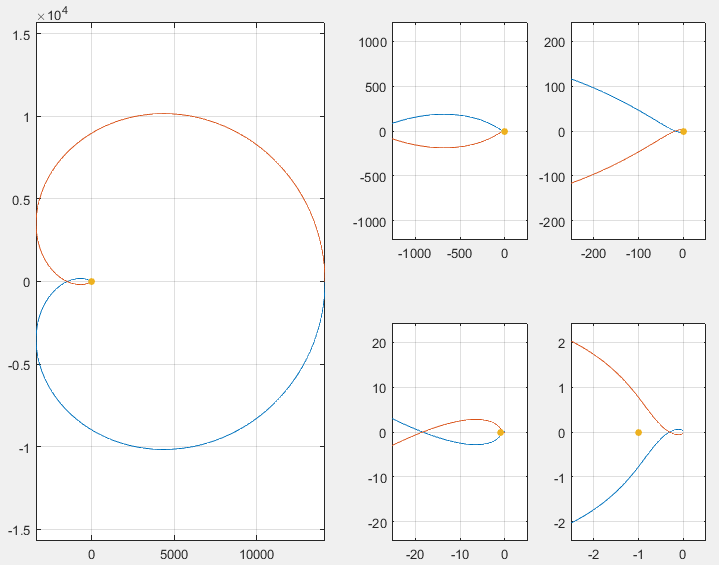
Nyquist_OPAMP_2

由于原始奈奎斯特图不方便查看，此处引入一个缩放函数

\[\begin{equation} f(x)=\left\{ \begin{aligned} sign(x)\cdot( \frac{1}{ln10}\cdot \vert x\vert ^3-(1+\frac{1}{ln10})\cdot \vert x\vert ^2+2\cdot \vert x\vert ), \vert x\vert <1 \\ sign(x)\cdot(log_{10}\vert x\vert ), \vert x\vert \geq1 \end{aligned} \right. \end{equation}\]

该缩放函数可以在尽量避免影响$-1<x<1$的前提下大大减小不同数量级之间的差别。在释加缩放函数后奈奎斯特曲线如下图所示（需要注意两条线实际上是连接在一起的，下同）。从这张图中便很容易观察出(-1, 0)没有被闭合曲线围绕（可以把曲线想象成柔软的绳子，而(-1, 0)是一根柱子，拉住最右侧部分的绳子向右拉动，可以发现绳子不会被柱子挡住），因此系统是稳定的。至于裕量，需要通过曲线与单位圆的交点进行判断，此处不再赘述。

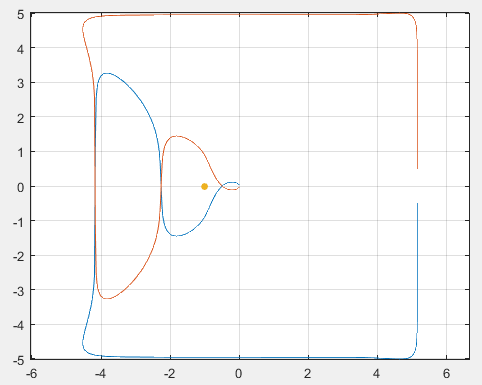
Nyquist_OPAMP_2_log

若将增益增大5倍，这条曲线会变成如下的样子，不难看出点(-1, 0)被沿逆时针方向围绕了两圈，即闭环传函在右半平面存在两个极点，系统不稳定。

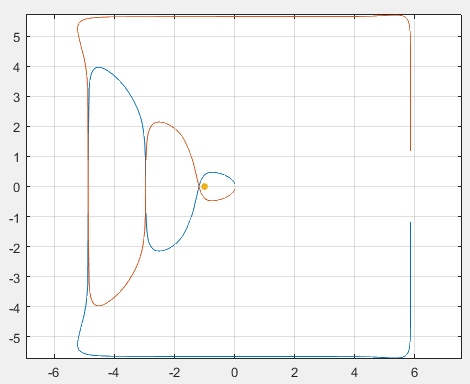
Nyquist_OPAMP_2_log2

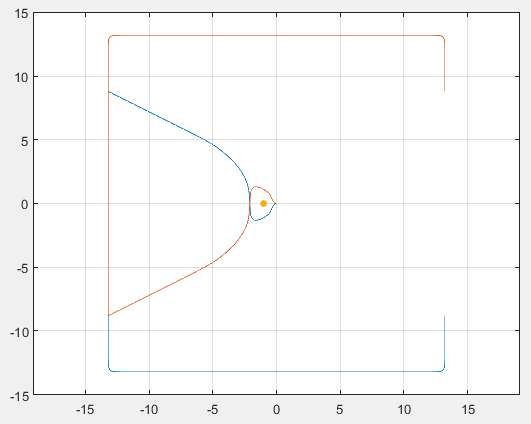
例2：考虑最前面带温度补偿的PLL，按照前面的规则绘制奈奎斯特图如下，同样可以看出点(-1, 0)没有被闭合曲线围绕，因此闭环系统是稳定的。

Nyquist_PLL_wTempCal_log

尼科尔斯图

前面提到的波特图和奈奎斯特图是以两种不同的方式展示$H(j\omega)$，分别是$\vert H(j \omega)\vert -\omega、\angle H(j \omega)-\omega$和$image(H(s))-real(H(s))$，而尼科尔斯图（Nichols Plot）是另外一种展示方式，它是$\vert H(j\omega)\vert -\angle H(j\omega)$曲线，如下图所示。

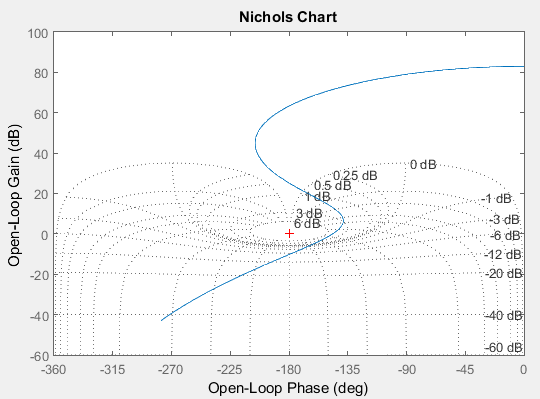
Nichols_OPAMP_2

波特图上的两条虚线就变成了尼科尔斯图上的一个点，一般情况下若点(-180$^\circ$, 0dB)在曲线的右侧（沿着$\omega$从小到大的方向看），则表示闭环系统稳定。而与波特图类似的，若相位多次穿过180$^\circ$，这种判据也会存在问题。

总结

本文的目的是探究负的增益裕量的含义和汇总常用的稳定性判据：

  • 增益裕量为负时闭环系统也可以是稳定的，只是说明若环路增益减小系统会进入不稳定状态，但如何直观的理解这一现象我还没找到答案；
  • 除了常见的巴克豪森判据，还有解析法、根轨迹法、奈奎斯特判据等方法可以稳妥的判断闭环系统是否稳定。
CATALOG
    FEATURED TAGS
    MATLAB PLL Programing Math Others Flask Training SerDes ChatGPT
    FRIENDS