模拟电路工程师不会对基于RLC的滤波器感到陌生,但对于数字滤波器或离散时间域滤波器就没那么熟悉了。今天我想总结一下简单的数字滤波器的分析方法、常用模拟滤波器对应的数字滤波器实现以及模拟滤波器的离散时间域建模方法。
模拟滤波器基本知识
模拟滤波器处理的是模拟信号,即对时间域上连续、电压域上也连续的信号进行处理。实现滤波功能的主要方式是利用电感、电容这类储能器件的特性,对于基于运算放大器的有源滤波器,还利用了反馈原理。
数字滤波器基本知识
基本结构
而数字滤波器处理的是数字信号,即对时间域上离散、电压域上也离散的信号进行处理,在数值与具体信号之间还存在编码问题。数字滤波器通常由乘法器、加法器和存储器构成。其中存储器通常用锁存器实现,框图上记为$z^{-1}$,即对输入进行了$T_s$的延迟,也称作“延1拍”或“打1拍”,这里的$T_s$为数字滤波器工作时钟的周期。
根据滤波器的输出是否会参与下一次运算,数字滤波器可以分为有限冲击响应(FIR)和无限冲击响应(IIR)两种。通俗地讲,就是看输出是由有限的输入决定,还是由在此之前所有的输入决定。如下图所示,对于FIR滤波器而言,当$n = j+1$时$Y[n]$便与$X[0]$没有关系了;而同样的情况下对于IIR滤波器而言,$X[0]$还可以通过$Y[n-1]$对$Y[n]$施加影响。
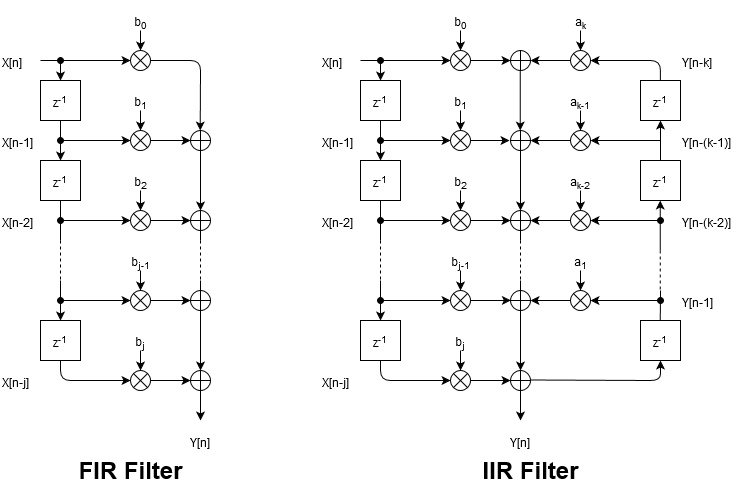
因为FIR滤波器不会无限地积累,因此它是绝对稳定的。但因为同样的原因,FIR滤波器不能实现DC处的极点。
频域响应
从上一节不难推出滤波器的传递函数:
- 对于FIR滤波器,有 \(Y[n]=\sum_{i=0}^{j}{b_iX[n-i]}\) \(\rightarrow Y[z]=\sum_{i=0}^{j}{b_iX[z]z^{-i}}\) \(\rightarrow H(z) = Y[z]/X[z] = \sum_{i=0}^{j}{b_iz^{-i}}\)
- 类似的,对于IIR滤波器,有 \(H(z) = Y[z]/X[z] = \sum_{i=0}^{j}{b_iz^{-i}} / (1 - \sum_{i=0}^{k}{a_iz^{-i}})\)
再将$z = e^{s\cdot T_s}, s=j\cdot\omega$代入即可计算出相应的频域响应。
需要注意的是,和数字信号一样,数字滤波器的传递函数也是周期延拓的,因此只需要看$0 \sim f_s/2$之间的即可。
常用滤波器的实现
下面列几种在模拟电路中常用的滤波器对应到数字域中的实现方法。
积分器
这个应该很容易想到,只要把输出延1拍后再送到输入相加即可,其框图可以表示如下:
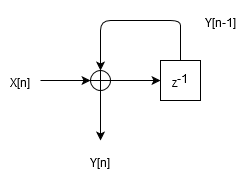
易得它的传递函数是$H(z) = 1/(1-z^{-1})$,将$z = e^{s\cdot T_s}$代入后可得$H(s)=1/(1-e^{-sT_s})$,当$sT_s«1$时做泰勒展开式替换便可得到$H(s)=1/(sT_s)=f_s/s$,即在低频处其传函与模拟积分器一致。下图所示的是数字滤波器和模拟滤波器实现的积分器的幅频和相频曲线对比(取$f_s=25MHz$,下同)。不难看出,当频率小于$f_s$一个数量级时幅频曲线吻合的很好,但相频曲线逐渐地出现了偏差。
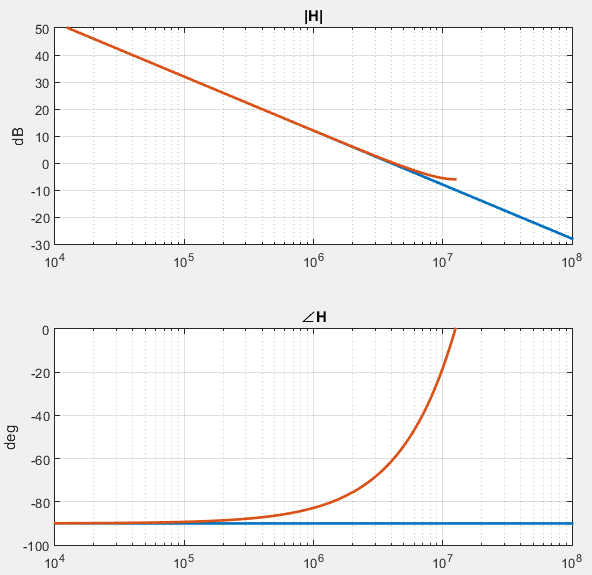
微分器/差分器
微分器也不难想到,用当前的输入减去上一次的输入即可,它的框图如下图所示:
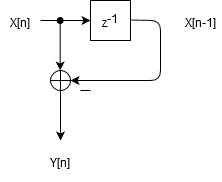
同样可得其传递函数为$H(z)=1-z^{-1}$,以及相应的频响曲线如下图所示:
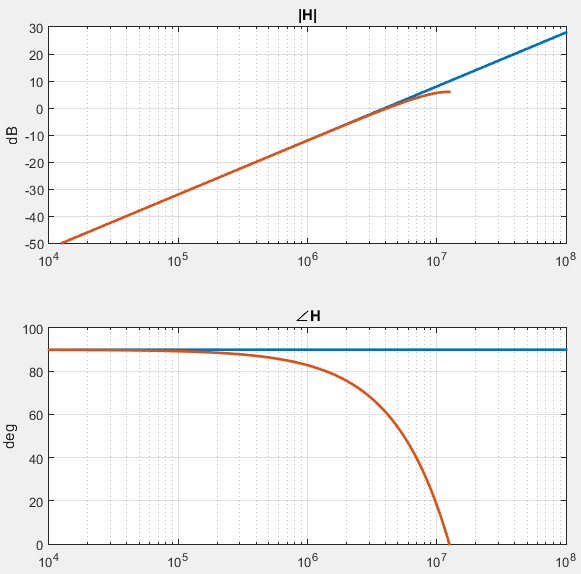
一阶RC低通滤波器
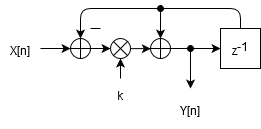
考虑如下图所示的一阶RC低通滤波器,电容上保持的电压(也就是当前$Y$的值)为$Y[n-1]$,经过一段很小的时间$\Delta t$后,有一定的电流经过电阻流向了电容,电流的大小为$I[N]=(X[N]-Y[n-1])/R$,那么电容上电压的变化值是$\Delta Y = I[N]\cdot \Delta t/C$,即当前的输出电压为 \(Y[n]=Y[n-1]+\Delta Y = Y[n-1]+(X[N]-Y[n-1])\cdot \Delta t/(RC)\)
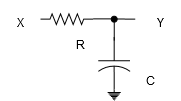
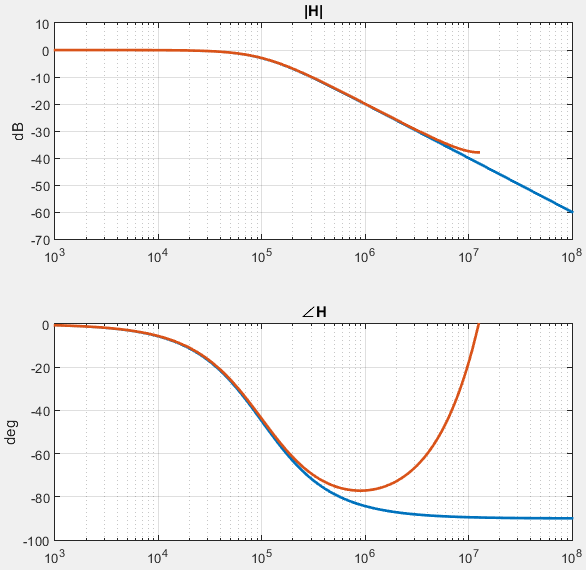
若把$\Delta t$当作$T_s$,便可得到对应数字滤波器的传函$H(z)=k/(1-(1-k)z^{-1})$,其中$k=T_s/(RC)$。其框图和频响曲线如下图所示:
一阶RC高通滤波器
由$H_{RC}=1-H_{CR}$,可得一阶RC高通滤波器的传递函数为
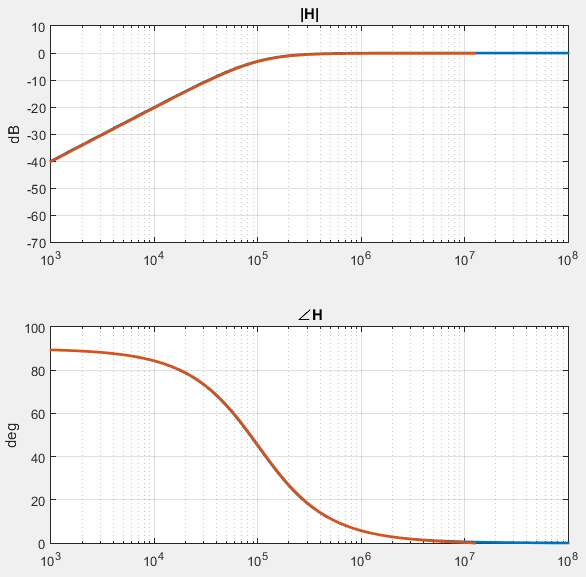
\[H(z)=1-k/(1-(1-k)z^{-1})=(1-k)(1-z^{-1})/(1-(1-k)z^{-1})\]对应的频响曲线如下图所示:
PID算法与级联
在自动控制领域,常用PID控制算法来处理反馈误差信号。其中P表示比例(proportional)、I表示积分(integral)、D表示微分(differential)。
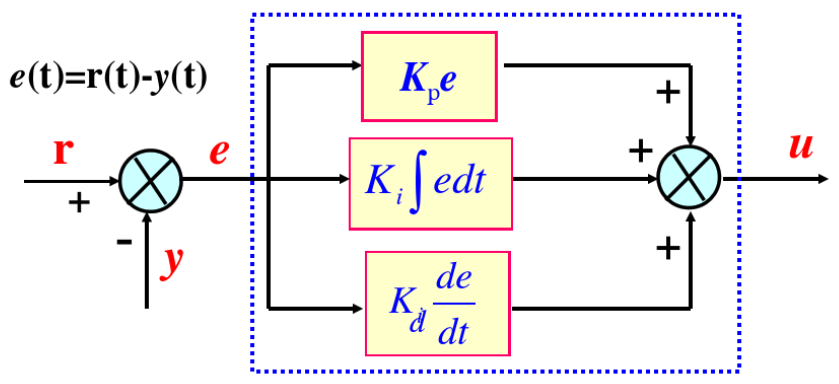
从幅频曲线的角度很容易理解,比例单元的幅频曲线是条水平直线,积分器和微分器的幅频曲线分别是斜向下方和斜向上方的直线,不同曲线叠加在一起时靠上部的会占主导。然后通过级联可以构成我们想要的频响,就像折纸一样。
在处理滤波器级联问题时需要注意几点与模拟滤波器不同的地方:
- 模拟滤波器存在负载效应,如两级RC滤波器级联后表现出来的极点与其各自单独工作时的不同,而数字滤波器不存在这个效应;
- 当数字滤波器级联时为了便于收敛时序通常需要锁存结果,这样会产生latency,导致更大的相位误差,在闭环使用时需要尤其注意;
- 对于固定的目标传递函数,滤波器的工作频率越高,频响越准确;
- 当数字滤波器与连续时间域的模块相连时,需要考虑零阶保持(ZOH)的影响,即级联$H_{ZOH}=(1-z^{-1})/(s\cdot T_s)$,它也会贡献额外的相移;
- 当不同工作频率的数字滤波器级联时即构成了
多采样率系统,需要在接口处增加抽样/插值器,并小心处理因此带来的镜像信号问题。
滞后超前滤波器
滞后超前滤波器是在type-II PLL中常用的环路滤波器,它的幅频曲线如下图所示:
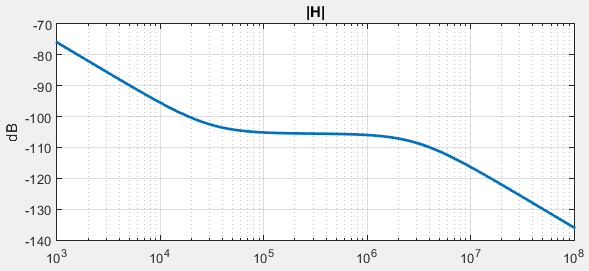
显然可以由一个积分单元加一个比例单元,再级联一个一阶低通组成。而一阶低通可以由积分单元加负反馈构成,整体的框图如下图所示(其中$k1=2\pi f_z/f_s, k2=2\pi f_p/f_s$):
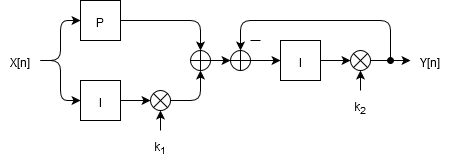
其对应的频响曲线如下图所示(其中$f_z=30kHz, f_p=1MHz, f_s=25MHz$)。可以看到相位在我们关心的地方是有几度的误差的,解决这个问题的唯一方案是提高$f_s$:
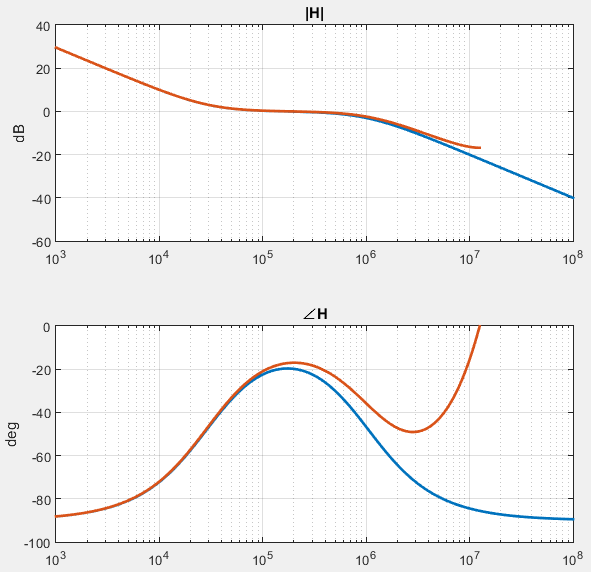
$f_s/2$频点陷波滤波器
前面举的几个例子好像都是模拟滤波器实现起来很简单,但数字滤波器很复杂的情况,接下来举一个模拟滤波器不方便做,而数字滤波器很轻松的例子。
$f_s/2$频点陷波滤波器,顾名思义即是只滤除在$f_s/2$处的单音干扰。其传函是$H(z)=(1+z^{-1})/2$,从传函上不难看出就是把相邻的两拍输入求平均,因此也叫移动平均(MA)。
在K线图上常见的MA5、MA20等也是类似的算法,但只是用来滤除高频扰动,而非单音干扰。
它的频响曲线如下图所示:
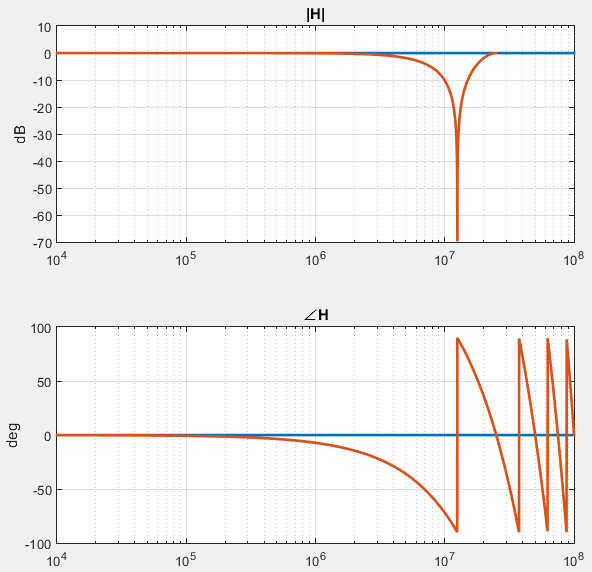
模拟滤波器的离散时间域建模
在对电路做行为级建模时,通常需要在离散时间域实现模拟滤波器的行为,以提高仿真效率。
如果可以写出滤波器的传递函数,便可以用上述的滤波器组合出来。而对于非常复杂的滤波器,则可以采用一种通用的方法实现。
- 首先根据电路的特性选择适合的$f_s$,一般不能小于最大极点频率的10倍;
- 然后给需要建模的电路施加阶跃响应,阶跃时的transition time不能小于$1/f_s$;
- 对电路的输出做采样,采样频率为$f_s$;
- 对采样结果求微分,并从阶跃处开始取值,直到接近0,得到一个序列$[b_i]$;
- 建立FIR滤波器,滤波器的系数即为$[b_i]$。
如果电路在DC处存在极点,可以先用理想器件把极点抵消掉再做仿真,建模时通过积分器级联FIR滤波器来实现。
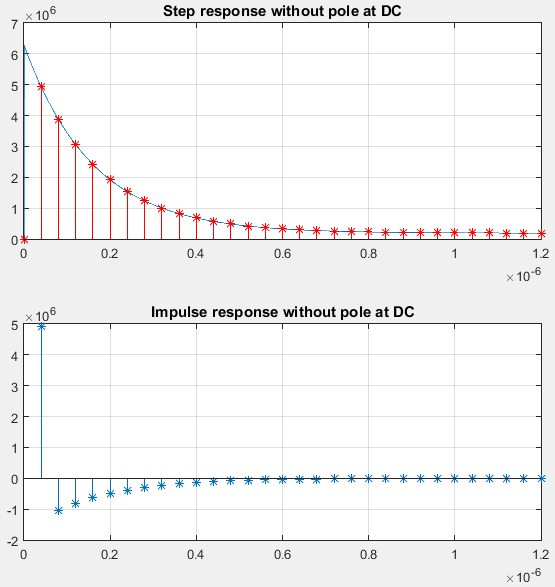
以PLL中的LPF为例,先把DC处的极点拿掉,仿真得到阶跃响应曲线,然后采样、求微分得到FIR滤波器的参数,如下图所示:
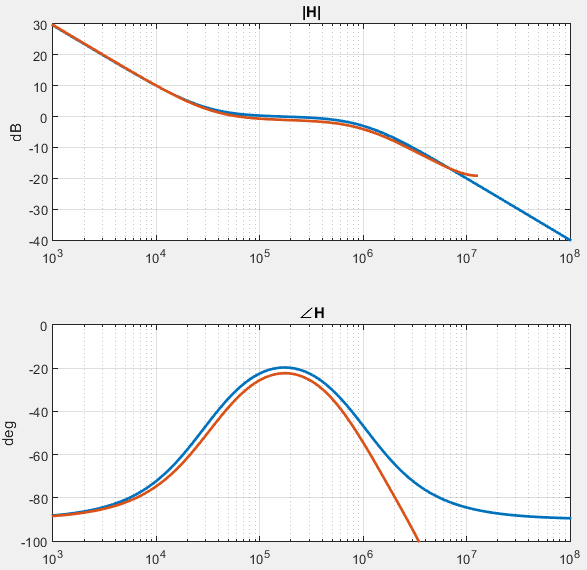
根据前面得到的参数配置FIR滤波器(FIR的工作频率为25MHz,阶数为30),并级联上积分器补回DC处的极点,得到最终的离散时间域滤波器模型。建模前后的频响曲线如下图所示:
如果将工作频率提升一倍,可以得到更好的效果,但此时FIR的阶数也要翻一番。
如果想通过给定幅频曲线直接产生滤波器参数,可以参考MATLAB中的firls函数。而且MATLAB还提供了连续时间域滤波器转换为离散时间域滤波器的函数c2d、bilinear等,其中也有很多有趣的细节,如果感兴趣可以自行查询资料,不再赘述。
至此,从模拟的角度对数字滤波器的总结告一段落,要知道真正在通信等领域用的数字滤波器更多是Butterworth、Chebyshev、Bessel、Elliptic等高阶滤波器,它们的设计可以参阅Signal Processing Toolbox中的滤波器部分。