基本原理
遗传算法(Genetic Algorithm,GA)的目的是解决最优化问题,基本原理则是模仿生物自然选择或进化的过程。
具体的,它把问题的解分成若干个基因,这些基因合为一个个体(也就是每个个体是一个潜在的解,每个基因是一个独立变量)。若干个体组成种群,通过一定的方式给种群中的每个个体打分(计算适应度),其中得分较高的部分个体(选择)可以繁殖产生后代。繁殖的过程包括杂交和变异,杂交表示新产生的个体的基因继承自两个长辈个体,变异表示基因会在原来的基础上产生一定的、随机的变化。选择和繁殖的过程会不断地改变群体里个体的基因,使其代表的解逐渐地向最优解靠近。
举个例子
通过遗传算法模拟生物外貌进化的过程。假设这种生物的外观也是RGB色彩空间的,我们通过选择与下图最相似的个体进行繁殖,看它们的演化过程是怎样的。
该图案是中央气象台nmc.cn的logo。

首先定义几个常数
# 每次选择出来的个体数
N_UNIT_TOP = 10
# 筛选代数(迭代次数)
N_LOOP = 1000
# 杂交时的交叉率:有多少比例的基因来自对方个体
RATE_CROSS = 0.4
# 变异率
RATE_CHANGE = 0.2
# 变异时的标准差
RATE_CHANGE_STD = 0.05
然后进行一些准备工作,包括读取参考图案、确定基因个数和种群大小、初始化记分牌之类的。
# 读取参考图案,确定基因个数和种群大小
pic_ref = plt.imread(FNAME_REF, format='png')
N_W, N_H, N_C = pic_ref.shape
N_GENE = N_W*N_H*3
N_UNIT = N_UNIT_TOP**2
# 记分牌
score_rcd = []
unit_rcd = []
unit_ref = pic_ref.reshape(N_GENE, 1)
接下来就是重头戏了,为了方便起见先把计算适应度和产生后代的过程写成函数。
# 计算适应度
def get_score(unit, unit_ref):
return sum((unit-unit_ref)**2)
# 产生后代
def gen_child(unit_x, unit_y):
idx = np.random.choice(range(N_GENE), int(RATE_CROSS*N_GENE))
idx2 = np.random.choice(range(N_GENE), int(RATE_CHANGE*N_GENE))
change = np.random.randn(N_GENE, 1)*RATE_CHANGE_STD
unit_new = copy(unit_x)
unit_new[idx] = unit_y[idx]
unit_new[idx2] += change[idx2]
unit_new = np.clip(unit_new, 0, 1)
return unit_new
遗传算法的主要部分是一个循环,每次循环做一次繁殖-适应-选择的迭代。
for i_loop in range(N_LOOP):
print(f'i = {i_loop+1} / {N_LOOP}')
# 繁殖
if i_loop==0:
# 初始化种群:通过随机
group = [np.random.random([N_GENE, 1]) for _ in range(N_UNIT)]
else:
# 杂交与变异:每两个不同的个体分别以自身为主、对方为辅进行杂交
for i_x in range(N_UNIT_TOP):
for i_y in range(N_UNIT_TOP):
if i_x==i_y:
continue
group.append(gen_child(group[i_x], group[i_y]))
# 打分(计算适应度)
scores = [get_score(u, unit_ref) for u in group]
# 选择,并记录下本轮中最佳的个体和得分
idx = [x[1] for x in sorted(zip(scores, range(N_UNIT)))]
score_rcd.append(scores[idx[0]])
unit_rcd.append(group[idx[0]])
group = [group[idx[i]] for i in range(N_UNIT_TOP)]
展示一下最终的结果:下图中左上角的为参考图案,其他的从左到右、从上到下是从初始一代到最后一代(相邻的两张图间隔了100代)各代中最佳的个体(即分最高的个体)。可以看到从完全没有图案到出现图案,再到图案逐渐清晰的过程。

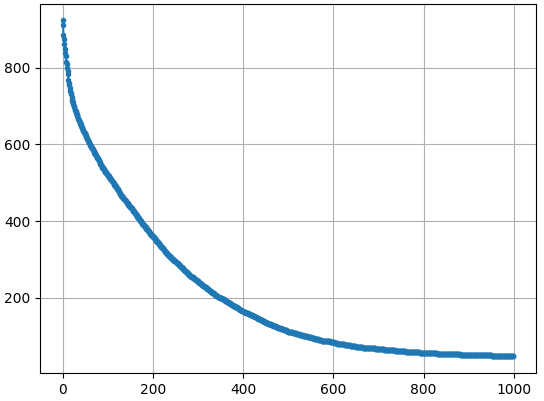
对应的各代最佳个体的分数变化如下图所示,可见600代后适应度分数的变化趋于平缓了,也对应了上图中图案清晰度的变化没那么大。
参考图案的尺寸是35x35像素,即基因的个数是3675个。在种群中个体的数量是100个、共迭代了1000代的情况下,耗时和各部分的比例如下。需要注意这个例子中计算适应度的函数非常简单,也就是说一般情况下产生新个体并不麻烦,评价个体的情况是花费时间最多的地方。
Generate: 74.49s (31.90%)
Score: 158.36s (67.82%)
Select: 0.64s (0.27%)
具体应用
具体到实现,第一步则是要把实际问题转化为可以用遗传算法求解的模型,这个模型有两个重要的组成部分:独立变量和评价方法。
如前面所说的,问题的解对应了算法中的“个体”,而其最小组成部分“基因“则对应了独立变量。实际问题里有些参数可能存在着关联,变量过多会导致求解困难,因此需要尽量提取其相互独立的部分。变量的取值可以是小数,也可以是整数,甚至是True/False。通过确定独立变量,便把解空间确定了下来。
求解过程实际上是一种搜索过程,要有一个能够判断解是否够好的量化方法,通过这个方法才能实现“选择”过程。
emmm……我本打算尝试用遗传算法去根据频率响应产生FIR滤波器参数,可是调了好久都没达到预期的效果,看来我还需要再学习一下。
一些思考
之所以看遗传算法,一方面是因为在网上看到类似枯叶蝶之类的动物(以及更多的自然界伪装高手 - 搜狐)时,总会有人说这么完美怎么可能是进化来的,一定是有“神”来设计。当然更多的人对这种观点是嗤之以鼻的,我就想可以借用遗传算法说明一下进化=随机突变+自然选择。

另一方面是因为近几年人工智能大火,点开IEEE TOP SERACHES就会看到有近一半关键词与人工智能或者机器学习相关;常逛的EETOP也被站长把“AI”设置成了关键词,普通单词里挨着的俩字母也经常会被误认而改成大写划上下划线,搞得莫名其妙。我想应该稍微去涉猎一下,免得被时代落下太多。而人工智能的三大模型(专家系统、遗传算法、神经网络,好像也有其他的说法)中遗传算法最为简洁、直接,便从这下了手。
以我个人目前浅显的调研来看,会影响到模拟集成电路设计领域的应该是专家系统模型,这也是最需要积累和普通电路设计者参与的模型,神经网络最多能在“小问题”和“模糊问题”上做一些加强。
神经网络的优势应该在于解“模糊问题”,如应对语音、手写文字、图像等等。这类问题的特点是很难用明确的方法得到解,而神经网络通过大量的参数和漫长的自动调参(训练)得到一组参数,使其能大概率地实现想要达到的目的。这种通用的方法看起来非常amazing,近几年飞速增长的算力也有了用武之地,但它的问题在于模型的训练要依赖大量的试错。在模拟集成电路设计中,有很多仿真需要较长的时间去覆盖所有的corner,诚然我们可以给出经验上的worst case来缩短这个过程,但可能也不是训练过程能接受的。
我想最可能的方法是把常用的电路结构量化分析透彻(比如经常被拿来举例的运算放大器和LDO),每个管子的功能和参数对整体的影响都写入“知识库”,这样当给出所需的规格时,计算机就可以根据“知识库”的信息自动找到最佳设计方案,甚至直接给出GDS。当换到一个未知的新工艺时,也只需要补充“知识库”的内容即可。打个比方,理论上DC和瞬态仿真是最精准的,用瞬态仿真也可以确定放大器的增益、噪声、稳定性等等,那为什么还需要小信号模型、反馈理论呢,还不是因为这样快嘛!因此我的观点是,模拟集成电路设计自动化的关键在于——抽象。要把实际工程中会用到的电路模块按类别抽象成模型,翻译成计算机能理解的“知识”。但这样相当于把训练神经网络变成了训练工程师,至少人的归纳、总结、演绎能力目前还是有优势……的吧?

