做时钟相关的，总是绕不过去相位噪声、抖动、EVM和眼图，今天再来捋一捋它们之间的“恩怨情仇”。

基本概念

相位噪声（Phase Noise）

在IEEE 1139-1999: IEEE Standard Definitions of Physical Quantities for Fundamental Frequency and Time Metrology—Random Instabilities中，相位噪声被明确定义如下：

2.6 phase deviation φ(t): Instantaneous phase departure from a nominal phase.

2.7 phase instability Sφ(f): One-sided spectral density of the phase deviation.

2.8 phase noise L(f): One-half of the phase instability Sφ(f).

从定义不难看出，相位噪声可以通过3步计算得到：

计算瞬时相位与标定相位的差值，得到相位偏移量。但实际测量中标定相位是不存在的，一般通过对待测信号进行拟合得到近似值。另外需要注意到，这里的相位以及相位偏移量都是连续信号。
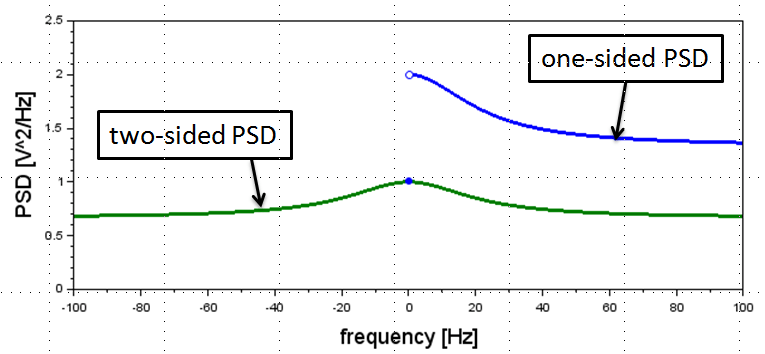
计算相位偏移量的单边谱密度，得到频域的相位不稳定性。关于单边谱和双边谱的示意如下图，双边谱即把能量铺到正负频率范围内，单边谱则只考虑正频率范围，因此单边谱的数值是双边谱的两倍。
简单地取相位不稳定性的一半作为相位噪声。由于相位偏移量是连续信号，且又不是周期信号，那么得到的谱密度必定是连续曲线。即从定义来说，1kHz的时钟信号可以有1MHz处的相位噪声。

但是历史上相位噪声是被定义为载波一定频偏处功率谱密度与载波功率的比值，也有单边带、双边带之分。

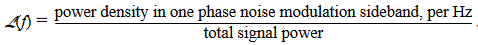
1642516090379

当说到单边带相位噪声（SSB phase noise）时指的是只考虑一侧的边带，即$f_0+f$或$f_0-f$处的功率谱密度减去载波功率（以dB为单位）；而当说到双边带相位噪声（DSB phase noise）时指的是考虑两侧的边带，因此就有$\mathcal{L}_{DSB}(f)=\mathcal{L}_{SSB}(f)+3\mathrm{dBc/Hz}$，正好与谱密度的定义相反……

为什么会这样？我个人的猜测是：对于频谱来说，只有复信号才必须考虑负频率范围的频谱，实信号的频谱在负频率与正频率范围只是镜像关系，很多时候没必要考虑。而对于载波的边带来说，在频谱上它永远是分布在载波两侧，只是看分析时是否要考虑进去。

那么问题就来了，Spectre中pnoise/hbnoise输出的phase noise是哪种？Keysight E5052B测试时显示的是哪种？

在用spectre仿真pnoise时，当选择Noise Type为sources时可以看到下方的提示为SSB。
根据E5052B的Manual，仪器显示的曲线是SSB phase noise，从它计算jitter的方式也可以看出来。（倒数第2行的$\pi$怎么显示的怪怪的）

因此，我们可以直接拿spectre的结果与测试结果进行对比，只是在计算jitter时记得乘2就好，就像上面的表格所示的。

抖动（Jitter）

在数字电路、采样电路与有线通信中，抖动是更常用来表示时钟质量的参数。在不同的应用场景下，关注的Jitter类型会有区别，体现在数值上也相去甚远。另外，考虑Jitter的时钟信号一定是Logic形式的，只有“沿”携带信息。

之前我有总结过一篇Jitter的基本知识，这次再做一下回顾和补充。

在提及Jitter的时候一定要记得它是一个统计量，因此要说明是范围（峰峰值，p2p）还是标准差（均方根，rms）。统计样本的不同则对应了不同的Jitter类型。

标准差（sdev）与均方根（rms）的定义不完全一样，二者的区别在于是否考虑DC分量上。由于我们计算Jitter时会去掉平均值，因此在这里时没有区别的。

Absolute Jitter

Absolute jitter（Jabs），也叫Phase jitter、TIE jitter等，指的是实际时钟沿出现的时刻与理想时钟沿出现的时刻之间的差。如计算Phase noise时需要的“标定相位”一样，“理想时钟沿”也是不存在的，一般通过对待测信号拟合得来。

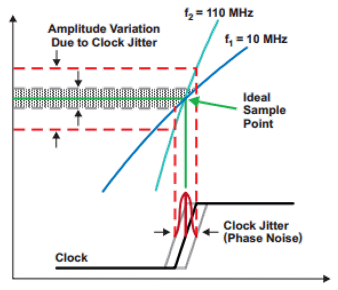
一般ADC、DAC应用关心这类Jitter的rms值，因为采样时钟的抖动会引起采样到的信号幅度的变化，进而恶化信噪比（SNR）。

1642903713203

Period Jitter

Period jitter（Jp），也叫Cycle jitter，指的是实际时钟周期与理想时钟周期的差，其平均值一般被当作频率偏移。

在数字电路、类DDR SerDes应用中关心这类Jitter的p2p值，因为时钟的抖动会引起Setup time/Hold time的减小。

需要注意在Jitter成分中有一类Periodic jitter（PJ），二者是完全不同的概念。Periodic jitter是“周期性的”抖动，即有规律的扰动，属于确定性抖动（DJ）的一种，是相对随机抖动（RJ）而言的。而Period jitter指的是计算Jitter时统计的样本为“周期”。

Cycle-to-cycle Jitter

Cycle-to-cycle jitter（Jc2c或Jcc），也叫Period-to-period jitter、Dperiod jitter等，指的是相邻的两个时钟周期的差。显然这类Jitter与时钟的整体情况机会没有关系，它只体现了非常短期（Short-term）的情况。

据说在Memory应用中关心这类Jitter。

N-Period Jitter

N-Period jitter，也叫N-cycle jitter、Accumulating jitter（Jacc）、Long-term jitter等，指的是连续N个周期总长时间与理想值的差，显然N=1时就是Period jitter。

对于提供同步时钟，但时钟频率低于数据速率的场景会关心这类抖动

EVM与IPN

EVM（Error Vector Magnitude，误差矢量幅度）是无线通信中常用的参数，它表示的是星座图（IQ constellation diagram）上Symbol的实际位置与理想位置的距离。幅度噪声会导致径向偏移，调制时钟的相位噪声则会导致周向偏移，二者都会导致信噪比的恶化。

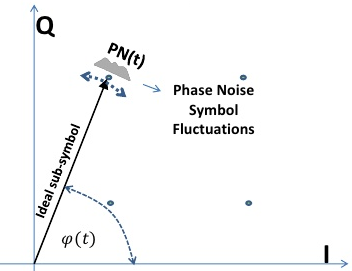
1642908029638

相位噪声对EVM的影响与Jabs对ADC SNR的非常相似，但是在星座图上是被归一化了的（即相对$2\pi$的大小），用秒为单位不太方便，更常用的参数是积分相位噪声（IPN）。类似于相位噪声，IPN同样有单边带、双边带之分，二者的数值上差3dB，E5052B上显示的是单边带IPN。

眼图（Eye Diagram）

眼图是有线通信中最常用的评估信号完整性（SI）的方法，具体的操作就是把波形逐单位间隔（UI）地叠加起来，再去看眼的大小。在叠眼的过程中，触发时钟（Trigger clock）与数据信号的关系对结果有非常重要的影响。

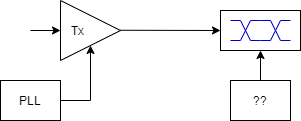
eye_digaram_clock

比如，如果Tx输出信号是用PLL输出clock的上升沿同步过的，在叠眼图时用同样的clock上升沿进行触发，那么看到的Jitter其实是Period jitter。如果用示波器内置的同频时钟（一般很难做到同频，除非把示波器与测试电路同步起来）进行触发，那么看到的Jitter其实是Absolute jitter。如果用一个环路自动追踪或恢复出clock作为触发时钟，环路的带宽与配置就会明显地影响看到的Jitter大小。

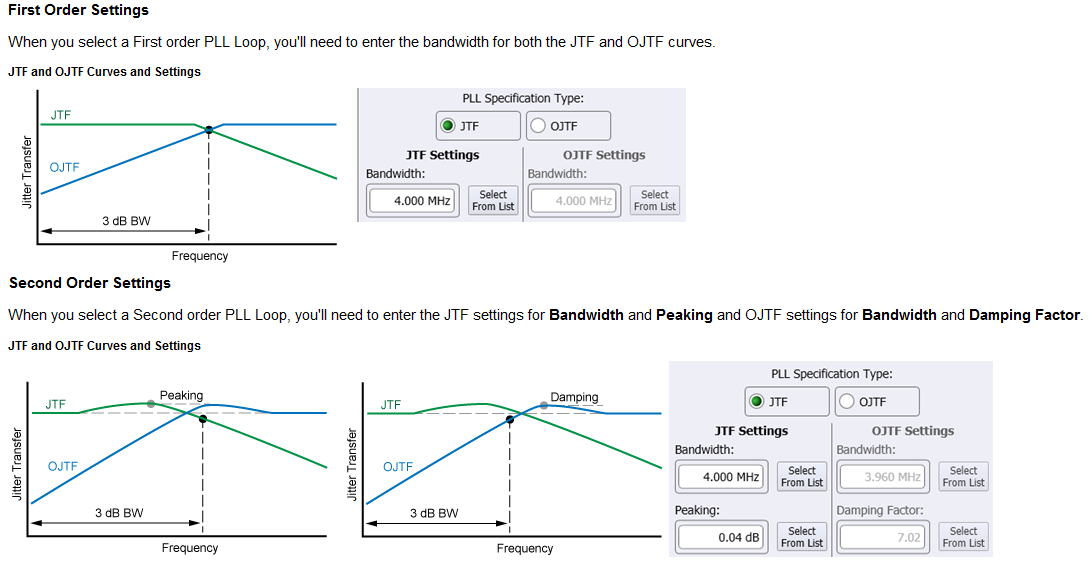
因此SerDes标准的兼容性测试规格（CTS）文档中会明确地写出来Golden CRU（时钟恢复单元）的参数，示波器也会提供相应的设置界面。如下图所示，对于一阶的Loop来说只需要提供带宽即可，对于二阶的Loop还要额外提供Peaking或者Damping factor的信息。

示波器的设置界面上会有两种类型的PLL Spec：低通的JTF和高通的OJTF，其实二者约束的是同一个环路，只不过是从两个不同的角度进行的。

1642935666545

Allan方差（Allan Variance）

Allan方差是一个在MEMS领域用的比较多的表示器件不稳定性的参数，它的计算方法是

设置一定的采样周期，分别计算采样周期内信号（频率或相位）的平均值；
再计算这些平均值中相邻两个的差值；
再计算这些差值的平方平均数得到方差；
以不同的采样周期重复上述步骤，最终得到各采样周期下的方差。

1642937052511

绘制成曲线，横轴是表示采样周期的时间，纵轴是方差，一般用log-log坐标显示。

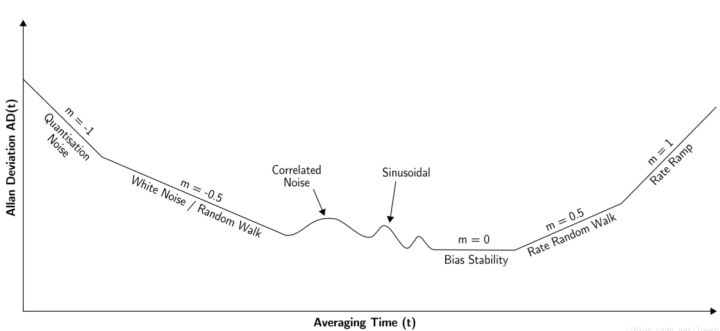
Allan方差在通信电路中不太常见（迄今为止只在32k RTC clock相关的测量中考虑过），在这只是提一下。

转换

对于同一个时钟信号，可以用不同的参数去描述其质量，这些参数之间可以进行转换。

抖动转相位噪声

我们通常说的抖动是一个数值，它能表示的信息量必然远小于相位噪声曲线，而此处说的抖动指的是统计的样本。

在介绍IEEE对相位噪声的定义时有提到，相位噪声是相位偏移量的谱密度，而对于Logic形式的时钟，只有沿处的相位是有意义的，如果我们有沿的偏移量数据，便可以得到相应的谱密度，即相位噪声。

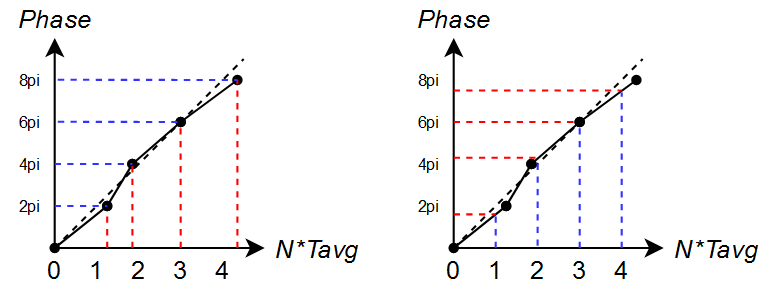
\[\mathcal{L}_{SSB}(f)=\frac{1}{2}{\rm{PSD}_{SSB}}(2\pi\Delta t[i]/T_{avg})\]

此处有个近似：时钟沿的时刻的物理含义应当如下图左边所示，即相位都是$2\pi$的整数倍，时间间隔是不均匀的；但在计算中是按照右侧的方式进行的，即时间间隔是均匀的，相位偏移了$2\pi\Delta t[i]/T_{avg}$。在抖动很小的情况下，每段的斜率都近似等于$2\pi/T_{avg}$，因此对结果的影响可以忽略。

因为$\Delta t[i]$是离散的实信号，那么其频谱只有在0~fs/2范围内有意义，而fs等于时钟的频率，也就是说对于1GHz的时钟信号，通过这种方式只能看到500MHz以内的相位噪声。一般来说也够用了，但对于有些场景还是要注意一下，比如SDM对分频器输出信号相位噪声的影响中便用到了这种方法计算SDM对MMD输出时钟相位噪声的影响，需要注意到高于fs/2的频偏处的相位噪声对于PLL来说仍然是有意义的。